题目内容
【题目】已知函数f（x）=x2﹣2lnx．
（1）求证：f（x）在（1，+∞）上单调递增．
（2）若f（x）≥2tx﹣ 
在x∈（0，1]内恒成立，求实数t的取值范围．
【答案】
（1）解：证明：函数的定义域为（0，+∞），f′（x）=2x﹣ 
= 
，
由f′（x）＞0，得x＞1，由f′（x）＜0，得0＜x＜1，
所以，函数f（x）在区间（1，+∞）上单调递增
（2）解：由f（x）≥2tx﹣ 
对x∈（0，1]恒成立，得2t≤x+ 
﹣ 
．
令h（x）=x+ ﹣ ，则h′（x）= 
，
因为x∈（0，1]，所以x4﹣3＜0，﹣2x2＜0，
2x2lnx＜0，x4＞0，
所以h′（x）＜0，
所以h（x）在（0，1）上为减函数．
所以当x=1时，h（x）=h（x）=x+ ﹣ ，有最小值2，得2t≤2，
所以t≤1，故t的取值范围是（﹣∞，1]
【解析】（1）先求函数的导数，根据导数和函数的单调性的关系即可求出，（2）要求若f（x）≥2tx﹣ 在x∈（0，1]内恒成立，即转化为2t≤x+ ﹣ 在x∈（0，1]内恒成立，只需求h（x）=x+ ﹣ x∈（0，1]内的最小值即可．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数
的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．
【题目】某校为了解校园安全教育系列活动的成效，对全校学生进行了一次安全意识测试，根据测试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记0分.现随机抽取部分学生的答卷，统计结果及对应的频率分布直方图如图所示：
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
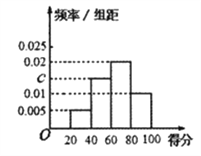
（Ⅰ）求
， 
， 
的值；
（Ⅱ）用分层抽样的方法，从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人，记所选4人的量化总分为
，求
的分布列及数学期望
；
（Ⅲ）某评估机构以指标
（
，其中
表示
的方差）来评估该校安全教育活动的成效.若
，则认定教育活动是有效的；否则认定教育活动无效，应调整安全教育方案.在（Ⅱ）的条件下，判断该校是否应调整安全教育方案？
