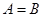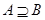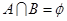题目内容
已知二次函数f(x)=ax2+x,若对任意x1,x2∈R,恒有2f(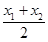 )≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
)≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
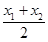 )≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
)≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
(1)(-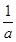 ,0) (2)(0,-2+
,0) (2)(0,-2+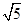 ]
]
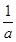 ,0) (2)(0,-2+
,0) (2)(0,-2+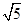 ]
]解:(1)对任意x1,x2∈R,
有f(x1)+f(x2)-2f(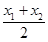 )=
)=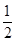 a(x1-x2)2≥0,
a(x1-x2)2≥0,
要使上式恒成立,∴a≥0.
由f(x)=ax2+x是二次函数知a≠0,故a>0.
由f(x)=ax2+x=ax(x+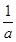 )<0,
)<0,
∴不等式f(x)<0的解集为A=(-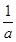 ,0).
,0).
(2)解得B=(-a-4,a-4),
∵B⊆A,
∴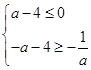
解得0<a≤-2+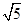 .
.
∴a的取值范围为(0,-2+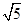 ].
].
有f(x1)+f(x2)-2f(
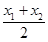 )=
)=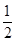 a(x1-x2)2≥0,
a(x1-x2)2≥0,要使上式恒成立,∴a≥0.
由f(x)=ax2+x是二次函数知a≠0,故a>0.
由f(x)=ax2+x=ax(x+
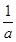 )<0,
)<0,∴不等式f(x)<0的解集为A=(-
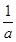 ,0).
,0).(2)解得B=(-a-4,a-4),
∵B⊆A,
∴
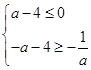
解得0<a≤-2+
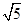 .
.∴a的取值范围为(0,-2+
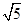 ].
].
练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
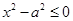 ,其中
,其中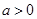 },B="{x|"
},B="{x|" 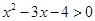 },且A
},且A 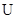 B = R,求实数
B = R,求实数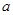 的取值范围.
的取值范围.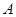 、
、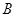 ,有下列四个命题:
,有下列四个命题: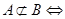 对任意
对任意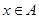 都有
都有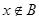 ;
;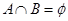 ;
;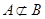
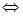
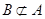 ;
;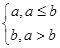 ,令f(x)=(cos2x+sinx)?
,令f(x)=(cos2x+sinx)?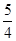 ,且x∈[0,
,且x∈[0,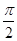 ],则函数f(x-
],则函数f(x-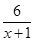 ≥1,x∈R},B={x|x2-2x-m<0}.
≥1,x∈R},B={x|x2-2x-m<0}.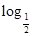 (x-1)>0},B={x|
(x-1)>0},B={x|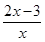 <0},则阴影部分表示的集合是( )
<0},则阴影部分表示的集合是( )
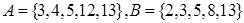 ,则
,则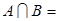 _______.
_______.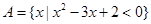 ,
,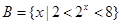 ,则( )
,则( )