题目内容
已知集合A={x|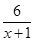 ≥1,x∈R},B={x|x2-2x-m<0}.
≥1,x∈R},B={x|x2-2x-m<0}.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
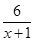 ≥1,x∈R},B={x|x2-2x-m<0}.
≥1,x∈R},B={x|x2-2x-m<0}.(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
(1){x|3≤x≤5} (2)8
解:由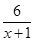 ≥1,得
≥1,得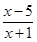 ≤0,∴-1<x≤5,
≤0,∴-1<x≤5,
∴A={x|-1<x≤5}.
(1)当m=3时,B={x|-1<x<3}.
则∁RB={x|x≤-1或x≥3},
∴A∩(∁RB)={x|3≤x≤5}.
(2) ∵A={x|-1<x≤5},A∩B={x|-1<x<4},
∴有42-2×4-m=0,解得m=8,
此时B={x|-2<x<4},符合题意.
故实数m的值为8.
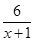 ≥1,得
≥1,得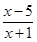 ≤0,∴-1<x≤5,
≤0,∴-1<x≤5,∴A={x|-1<x≤5}.
(1)当m=3时,B={x|-1<x<3}.
则∁RB={x|x≤-1或x≥3},
∴A∩(∁RB)={x|3≤x≤5}.
(2) ∵A={x|-1<x≤5},A∩B={x|-1<x<4},
∴有42-2×4-m=0,解得m=8,
此时B={x|-2<x<4},符合题意.
故实数m的值为8.

练习册系列答案
相关题目
 ,
,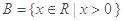 ,则
,则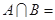 ( )
( )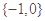
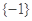
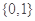
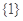
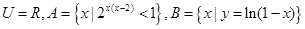 ,则阴影部分表示的集合为( )
,则阴影部分表示的集合为( )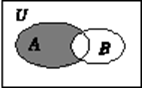
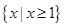
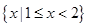
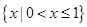
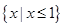
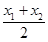 )≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
)≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.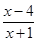 ≤0},B={x∈R|(x-2a)(x-a2-1)<0}.若A∩B=∅,则实数a的取值范围是( )
≤0},B={x∈R|(x-2a)(x-a2-1)<0}.若A∩B=∅,则实数a的取值范围是( )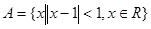 ,
,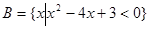 ,则
,则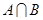 =_____
=_____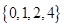 ,B=
,B=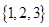 ,则
,则 ( )
( )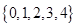
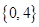

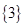
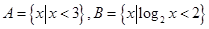 ,则
,则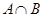 =( )
=( )