题目内容
7.已知等比数列{an}的公比q>1,前n项和为Sn,并且满足a2+a3+a4=28,a3+2是a2和a4的等差中项.(1)求数列{an}的通项公式;
(2)若bn=anlog${\;}_{\frac{1}{2}}$an,Sn=b1+b2+…+bn,求使Sn>254-n•2n+1成立的正整数n的最小值.
分析 (1)依题意有2(a3+2)=a2+a4,又a2+a3+a4=28,故a3=8.a2+a4=20.由此能够推导出an=2n.
(2)bn=anlog${\;}_{\frac{1}{2}}$an=2n•$lo{g}_{\frac{1}{2}}$2n=-n•2n,由错位相减法可得Sn,再由Sn>254-n•2n+1,解不等式即可得到n的最小值.
解答 解:(1)依题意有2(a3+2)=a2+a4,
又a2+a3+a4=28,解得3=8.
所以a2+a4=20.
于是有$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}{q}^{3}=20}\\{{a}_{1}{q}^{2}=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{q=2}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=32}\\{q=\frac{1}{2}}\end{array}\right.$,
又{an}是递增的,故a1=2,q=2.
所以an=2n.
(2)bn=anlog${\;}_{\frac{1}{2}}$an=2n•$lo{g}_{\frac{1}{2}}$2n=-n•2n,
-Sn=1•2+2•22+3•23+…+n•2n,
-2Sn=1•22+2•23+3•24+…+n•2n+1,
相减可得Sn=2+22+23+…+2n-n•2n+1
=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1=2n+1-2-n•2n+1,
由Sn>254-n•2n+1,可得2n+1>256=28,
即为n+1>8,即n>7,
则n的最小值为8.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,解题时要认真审题,注意挖掘题设中的隐含条件,灵活地运用公式解答.

| A. | μ=$\frac{k-n}{k-m}$ | B. | μ=$\frac{n-m}{n-k}$ | C. | μ=$\frac{n-m}{k-m}$ | D. | μ=$\frac{k-m}{k-n}$ |
| A. | 10个教职工中,必有1人当选 | |
| B. | 每位教职工当选的可能性是$\frac{1}{10}$ | |
| C. | 数学教研组共有50人,该组当选教工代表的人数一定是5 | |
| D. | 以上说法都不正确 |
| A. | (-∞,$\frac{5}{4}$) | B. | (-∞,$\frac{5}{4}$] | C. | ($\frac{5}{4}$,+∞) | D. | [$\frac{5}{4}$,+∞) |
| A. | A?B | B. | B?A | C. | A=B | D. | A∩B=Φ |
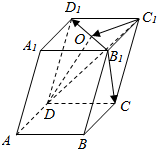 如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.
如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.