题目内容
17.已知等差数列{an}的前n项和为Sn,向量$\overrightarrow{OP}$=(n,$\frac{{S}_{n}}{n}$),$\overrightarrow{O{P}_{1}}$=(m,$\frac{{S}_{m}}{m}$),$\overrightarrow{O{P}_{2}}$=(k,$\frac{{S}_{k}}{k}$),且$\overrightarrow{OP}$=λ$\overrightarrow{O{P}_{1}}$+μ$\overrightarrow{O{P}_{2}}$,已知m,n,k∈N*且互不相等,则用m,n,k表示μ=( )| A. | μ=$\frac{k-n}{k-m}$ | B. | μ=$\frac{n-m}{n-k}$ | C. | μ=$\frac{n-m}{k-m}$ | D. | μ=$\frac{k-m}{k-n}$ |
分析 $\overrightarrow{OP}$=λ$\overrightarrow{O{P}_{1}}$+μ$\overrightarrow{O{P}_{2}}$,可得n=λm+μk,$\frac{{S}_{n}}{n}$=$\frac{λ{S}_{m}}{m}$+$\frac{μ{S}_{k}}{k}$,化为:μ=$\frac{n(\frac{{S}_{n}}{{n}^{2}}-\frac{{S}_{m}}{{m}^{2}})}{k(\frac{{S}_{k}}{{k}^{2}}-\frac{{S}_{m}}{{m}^{2}})}$,利用等差数列的前n项和公式可得:$\frac{{S}_{n}}{{n}^{2}}-\frac{{S}_{m}}{{m}^{2}}$=$\frac{(m-n)(2{a}_{1}-d)}{2mn}$,$\frac{{S}_{k}}{{k}^{2}}-\frac{{S}_{m}}{{m}^{2}}$=$\frac{(m-k)(2{a}_{1}-d)}{2mk}$,即可得出.
解答 解:∵$\overrightarrow{OP}$=λ$\overrightarrow{O{P}_{1}}$+μ$\overrightarrow{O{P}_{2}}$,
∴n=λm+μk,$\frac{{S}_{n}}{n}$=$\frac{λ{S}_{m}}{m}$+$\frac{μ{S}_{k}}{k}$,
∴$\frac{{S}_{n}}{n}=\frac{{S}_{m}}{m}×\frac{n-μk}{m}$+$\frac{μ{S}_{k}}{k}$,
化为:μ=$\frac{n(\frac{{S}_{n}}{{n}^{2}}-\frac{{S}_{m}}{{m}^{2}})}{k(\frac{{S}_{k}}{{k}^{2}}-\frac{{S}_{m}}{{m}^{2}})}$,
∵等差数列{an}的前n项和为Sn,
∴$\frac{{S}_{n}}{{n}^{2}}-\frac{{S}_{m}}{{m}^{2}}$=$\frac{n{a}_{1}+\frac{n(n-1)d}{2}}{{n}^{2}}$-$\frac{m{a}_{1}+\frac{m(m-1)d}{2}}{{m}^{2}}$=$\frac{(m-n)(2{a}_{1}-d)}{2mn}$,
同理可得:$\frac{{S}_{k}}{{k}^{2}}-\frac{{S}_{m}}{{m}^{2}}$=$\frac{(m-k)(2{a}_{1}-d)}{2mk}$,
∴μ=$\frac{m-n}{m-k}$=$\frac{n-m}{k-m}$.
故选:C.
点评 本题考查了等差数列的前n项和公式、向量的线性运算性质,考查了推理能力与计算能力,属于中档题.

| A. | i | B. | -i | C. | 1 | D. | -1 |
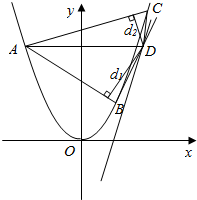 (理科)如图,A,B,C,D在y=$\frac{1}{4}$x2上,A、D关于抛物线对称轴对称,过点D(x0,y0)作抛物线切线,可证切线斜率为$\frac{1}{2}$x0,BC∥切线,点D到AB,AC距离分别为d1,d2,d1+d2=$\sqrt{2}$|AD|
(理科)如图,A,B,C,D在y=$\frac{1}{4}$x2上,A、D关于抛物线对称轴对称,过点D(x0,y0)作抛物线切线,可证切线斜率为$\frac{1}{2}$x0,BC∥切线,点D到AB,AC距离分别为d1,d2,d1+d2=$\sqrt{2}$|AD|