题目内容

14．设集合A={m-2，-3}，B={-1，m-3}，若A∩B={-3}，则m的值为0．

分析 由A与B，以及两集合的交集确定出m的值即可．

解答 解：∵A={m-2，-3}，B={-1，m-3}，且A∩B={-3}，
∴m-3=-3，
解得：m=0，
故答案为：0

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
4．已知集合U={1，2，3，4，5，6，7}，A={x∈R|数轴上x到3的距离等于1，或x到6的距离等于1}，B={x∈Z|$\frac{2x-11}{2-x}≥0$}，求（∁UA）∪（∁UB）．
5．圆C：x2+y2-6x-8y+23=0的半径为（　　）
A．$\sqrt{2}$B．2C．2$\sqrt{2}$D．4
2．各项均为正数的等比数列{an}，a1=1，a2a4=16，数列{bn}的前n项和为Sn，且Sn=$\frac{3{n}^{2}+n}{2}$（n∈N+）．
（1）求数列{an}，{bn}的通项公式；
（2）cn=anbn（n∈N+），求数列{cn}的前n项和Tn；
（3）若dn=an+（-1）nbn，设数列{dn}的前n项和为Un，求Un．
9．下列命题中，正确的是（　　）
A．$\overrightarrow{a}$与$\overrightarrow{b}$共线，$\overrightarrow{b}$与$\overrightarrow{c}$共线，则$\overrightarrow{a}$与$\overrightarrow{c}$也共线
B．任意两个相等的非零向量的始点与终点总是一平行四边形的四个顶点
C．向量$\overrightarrow{a}$与$\overrightarrow{b}$不共线，则$\overrightarrow{a}$与$\overrightarrow{b}$都是非零向量
D．有相同起点的两个非零向量不平行
19．（1）求值：${8^{\frac{2}{3}}}+{2^{{{log}_2}3}}+{（{\frac{1}{4}}）^0}$；
（2）已知${x^{\frac{1}{2}}}+{x^{-\frac{1}{2}}}=4$，求x+x-1的值．
6．若方程16x2+ky2=16k表示焦点在y轴上的椭圆，则实数k的取值范围是（0，16）．
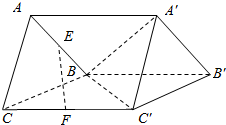3．如图，三棱柱ABC-A′B′C′，E，F分别是AB，CC′的中点，过EF作一个平面和面A′BC′相交，并找到交线，写出作法．（注意：交线必须是由两个确定的点的连线）
4．若y=log2（x+a）的反函数的图象经过点P（-1，0），则实数a的值为（　　）
A．-2B．2C．-$\frac{1}{2}$D．$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网