题目内容
3.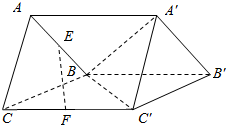 如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
分析 取AA′中点G,A′B中点H,连结EG、FG、EH、C′H,过EF作一个平面和面A′BC′相交,交线为HC′.
解答 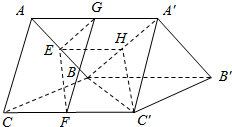 解:取AA′中点G,A′B中点H,连结EG、FG、EH、C′H,
解:取AA′中点G,A′B中点H,连结EG、FG、EH、C′H,
∵三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,
∴EG∥BA′,FG∥C′A′,
∵EG∩FG=G,BA′∩C′A′=A′,
∴面EFG∥A′BC′,
∵E、H、F分别是AB、A′B、CC′的中点,ACC′A′是平行四边形,
∴EH$\underset{∥}{=}$FC′,∴FC′HE是平行四边形,
∴EF∥HC′,
∵过EF作一个平面和面A′BC′相交,
∴交线为HC′.
点评 本题考查两平面相交的交线的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
15.若直线过点(-1,1),(2,2),则此直线的斜率为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | -$\frac{1}{3}$ |
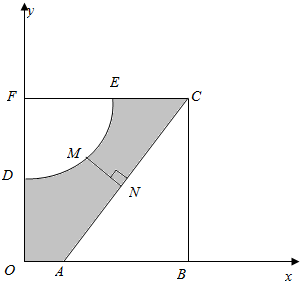 如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分. 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为$\frac{1}{2}$.过原点的直线与椭圆C交于A、B两点(A,B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为$\frac{1}{2}$.过原点的直线与椭圆C交于A、B两点(A,B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB.