题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,直线
,直线![]() :
: ![]() 与以原点为圆心、椭圆
与以原点为圆心、椭圆![]() 的短半轴长为半径的圆
的短半轴长为半径的圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,与圆
,与圆![]() 相交于两点
相交于两点![]() ,
, ![]() ,若
,若![]() 是钝角三角形,求直线
是钝角三角形,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() ,且
,且![]()
【解析】试题分析:(1)先由离心率为![]() ,求出
,求出![]() 的关系,再利用直线
的关系,再利用直线![]()
![]() 与以原点为圆心、椭圆
与以原点为圆心、椭圆![]() 的短半轴长为半径的圆
的短半轴长为半径的圆![]() 相切,求出
相切,求出![]() 即可求出椭圆的方程;(2)先设出
即可求出椭圆的方程;(2)先设出![]() 的坐标,利用
的坐标,利用![]() 是钝角三角形,可得
是钝角三角形,可得![]() ,即
,即![]() ,联立方程写出韦达定理代入,从而求得斜率
,联立方程写出韦达定理代入,从而求得斜率![]() 的取值范围.
的取值范围.
试题解析:(1)由![]() ,得
,得![]() ,
,
由直线![]()
![]() 与圆
与圆![]() 相切,得
相切,得![]() 所以
所以![]() ,
, ![]() ,
,
所以椭圆的方程是![]() .
.
(2)由(1),得圆![]() 的方程是
的方程是![]() ,
, ![]() ,直线
,直线![]() 的方程是
的方程是![]()
设![]() ,
, ![]() ,由
,由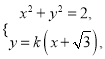 得
得![]()
则![]() ,
, ![]() .
.
由![]() ,得
,得![]() .①
.①
因为![]() 是钝角三角形,所以
是钝角三角形,所以![]() ,即
,即![]()
![]()
![]()
![]()
所以![]() .②
.②
由![]() ,
, ![]() 与
与![]() 轴不共线,知
轴不共线,知![]() .③
.③
由①、②、③,得直线![]() 的斜率
的斜率![]() 的取值范围是
的取值范围是![]() ,且
,且![]() .
.

练习册系列答案
相关题目
【题目】上半年产品产量与单位成本资料如下:
月份 | 产量/千件 | 单位成本/元 |
1 | 2 | 73 |
2 | 3 | 72 |
3 | 4 | 71 |
4 | 3 | 73 |
5 | 4 | 69 |
6 | 5 | 68 |
且已知产量x与单位成本y具有线性相关关系.
(1)求出回归方程.
(2)指出产量每增加1 000件时,单位成本平均变动多少?
(3)假定产量为6 000件时,单位成本为多少元?