题目内容
【题目】成等差数列的三个正数的和等于15，并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(1)求数列{bn}的通项公式；
(2)数列{bn}的前n项和为Sn，求证：数列
是等比数列.
【答案】见解析
【解析】
(1)解 设成等差数列的三个正数分别为a－d，a，a＋d.
依题意，得a－d＋a＋a＋d＝15.
解得a＝5.
所以{bn}中的b3，b4，b5依次为7－d，10，18＋d.
依题意，有(7－d)(18＋d)＝100，
解得d＝2或d＝－13(舍去).
故{bn}的第3项为5，公比为2.
由b3＝b1·22，即5＝b1·22，
解得b1＝
.
所以bn＝b1·qn－1＝·2n－1＝5·2n－3，
即数列{bn}的通项公式bn＝5·2n－3.
(2)证明 由(1)得数列{bn}的前n项和
Sn＝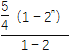
＝5·2n－2－，即Sn＋＝5·2n－2.
所以S1＋＝
，
＝
＝2.
因此
是以为首项，2为公比的等比数列.
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
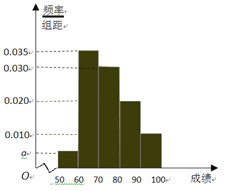
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
