题目内容
设椭圆方程为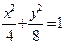 ,过原点且倾斜角为
,过原点且倾斜角为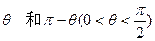 的两条直线分别交椭圆于A、C和B、D两点.(1)用
的两条直线分别交椭圆于A、C和B、D两点.(1)用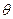 表示四边形ABCD的面积S;(2)当
表示四边形ABCD的面积S;(2)当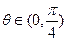 时,求S的最大值.
时,求S的最大值.
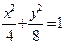 ,过原点且倾斜角为
,过原点且倾斜角为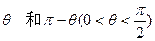 的两条直线分别交椭圆于A、C和B、D两点.(1)用
的两条直线分别交椭圆于A、C和B、D两点.(1)用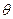 表示四边形ABCD的面积S;(2)当
表示四边形ABCD的面积S;(2)当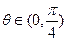 时,求S的最大值.
时,求S的最大值.(1)四边形ABCD的面积S=4| xy|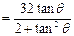 ;(2)
;(2) .
.
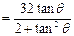 ;(2)
;(2) .
.(1)设经过原点且倾斜角为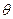 的直线方程为y= x tan
的直线方程为y= x tan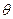 ,代入
,代入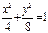 ,
,
求得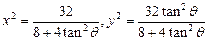 .
.
由对称性可知四边ABCD为矩形,又由于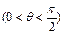 ,
,
所以四边形ABCD的面积S=4| xy|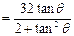 .
.
(2)当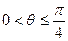 时,
时,  ,设t=tan
,设t=tan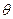 ,则S
,则S
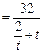 ,
,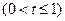
设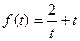 ,因为
,因为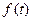 在(0,1]上是减函数,所以
在(0,1]上是减函数,所以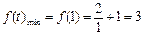 .
.
所以,当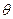 =
=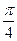 时,
时, .
.
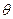 的直线方程为y= x tan
的直线方程为y= x tan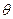 ,代入
,代入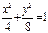 ,
,求得
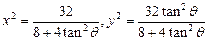 .
.由对称性可知四边ABCD为矩形,又由于
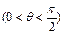 ,
,所以四边形ABCD的面积S=4| xy|
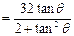 .
.(2)当
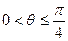 时,
时,  ,设t=tan
,设t=tan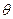 ,则S
,则S
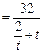 ,
,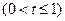
设
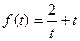 ,因为
,因为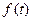 在(0,1]上是减函数,所以
在(0,1]上是减函数,所以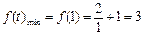 .
.所以,当
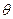 =
=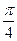 时,
时, .
.
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
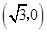 ,一条渐近线m:
,一条渐近线m: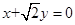 ,设过点A
,设过点A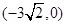 的直线l的方向向量
的直线l的方向向量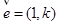 。
。 ,且a与l的距离为
,且a与l的距离为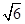 ,求K的值;
,求K的值;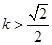 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为 ⊥x轴于点C,
⊥x轴于点C,  ,
, ,动点
,动点 到直线
到直线
 交点
交点 两点(
两点(
 满足
满足 ,求直线
,求直线 的斜率的取值范围
的斜率的取值范围
 、
、 满足
满足 则
则 的最大值为( )
的最大值为( )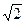 ),对应的准线方程为y=-
),对应的准线方程为y=-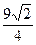 ,且离心率e满足:
,且离心率e满足: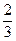 ,e,
,e,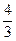 成等比数列.
成等比数列.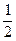
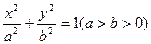 的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且
的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且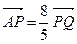
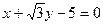 相切,求椭圆C的方程.
相切,求椭圆C的方程. 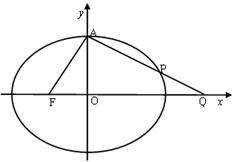
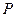
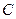
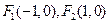
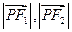
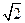

 之间的“直角距离”为
之间的“直角距离”为 。若
。若 到点
到点 的“直角距离”相等,其中实数
的“直角距离”相等,其中实数 满足
满足 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长度之和为
的轨迹的长度之和为