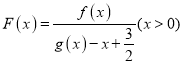题目内容
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
【答案】(1)![]() ,答案不唯一(2)证明见解析(3)
,答案不唯一(2)证明见解析(3)![]() ,证明见解析
,证明见解析
【解析】
(1)令![]() ,由于
,由于![]() ,则可证明;
,则可证明;
(2)根据题意可知![]() ,再根据函数的单调性即可证明;
,再根据函数的单调性即可证明;
(3)由题得![]() ,可得
,可得![]() 结合数学归纳法得到
结合数学归纳法得到![]() ,即可得证.
,即可得证.
(1)![]() ,
,
∴![]() 为“关于2的偶型函数”.
为“关于2的偶型函数”.
(2)![]() .
.
任取![]() 则
则![]() ,因为函数在
,因为函数在![]() 单调递增,所以
单调递增,所以![]() .所以函数在
.所以函数在![]() 上单调递减
上单调递减
(3)猜测![]()
![]() 数学归纳法证明:
数学归纳法证明:
1.当![]() 时
时![]() 因为
因为![]() 是奇函数,所以
是奇函数,所以![]() 得证
得证
2.假设当![]() ,
,![]() 成立,
成立,
因为![]() ,
,
又∵奇函数,∴![]() ,
,
∴当![]() 时,
时,![]() ,所以得证.
,所以得证.

练习册系列答案
相关题目