题目内容
已知函数f(x)＝
x4－2x3＋3m，x∈R，若f(x)＋9≥0恒成立，则实数m的取值范围是( )
A．m≥ | B．m> | C．m≤ | D．m< |
A
解析试题分析：因为函数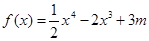
），所以
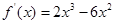．令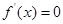
得x=0或x=3，经检验知x=3是函数的一个最小值点，所以函数的最小值为
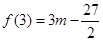．不等式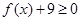
恒成立，即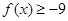
恒成立，所以
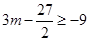，解得
．故答案选A．
考点：1、函数恒成立问题；2、利用导数求闭区间上函数的最值.
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
若函数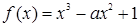
在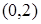
上单调递减，则实数
的取值范围为（ ）
A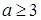． | B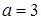． | C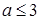． | D． |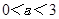
下列四个函数，在x=0处取得极值的函数是（ ）
①y=x3 ②y=x2+1 ③y=|x| ④y=2x
| A．①② | B．②③ | C．③④ | D．①③ |
设曲线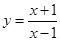
在点(3,2)处的切线与直线
垂直，则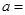
| A．2 | B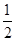． | C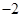． | D． |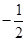
，x＝
函数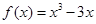
在区间
上( )
| A．有最大值，但无最小值 |
| B．有最大值，也有最小值 |
| C．无最大值，但有最小值 |
| D．既无最大值，也无最小值． |
函数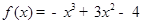
的单调递增区间是 （ ）
A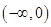． | B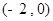． | C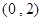． | D． |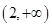
[2014·汕头模拟]设f(x)＝
，则
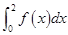等于( )
A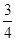． | B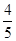． | C． | D．不存在 |
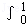（ex+2x）dx等于（ ）
| A．1 | B．e﹣1 | C．e | D．e2+1 |