题目内容
若函数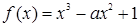 在
在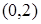 上单调递减,则实数
上单调递减,则实数 的取值范围为( )
的取值范围为( )
A.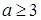 | B.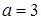 | C.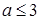 | D.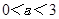 |
A
解析试题分析: ,因为函数
,因为函数 在
在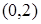 上单调递减,则在
上单调递减,则在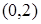 上
上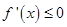 即
即 恒成立,等价于
恒成立,等价于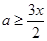 在
在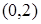 上恒成立,所以
上恒成立,所以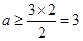 。故A正确。
。故A正确。
考点:用导数研究函数的性质。

练习册系列答案
相关题目
函数 的极大值为
的极大值为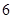 ,那么
,那么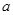 的值是( )
的值是( )
A.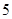 | B. | C.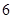 | D. |
已知函数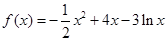 在
在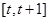 上不单调,则
上不单调,则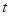 的取值范围是( )
的取值范围是( )
A. | B.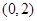 | C. | D. |
曲线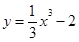 在点
在点 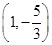 处切线的斜率为( )
处切线的斜率为( )
A. | B. | C. | D. |
若函数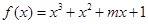 是R上的单调函数,则实数m的取值范围是( )。
是R上的单调函数,则实数m的取值范围是( )。
A. | B. | C. | D.  |
定义在R上的可导函数 f(x)=x2 + 2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,
则m的取值范围是( )
| A.m≥2 | B.2≤m≤4 | C.m≥4 | D.4≤m≤8 |
函数 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数f(x)= x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是( )
x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是( )
A.m≥ | B.m> | C.m≤ | D.m< |
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)<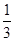 ,则f(x)<
,则f(x)< +
+ 的解集为( )
的解集为( )
| A.{x|-1<x<1} | B.{x|x<-1} |
| C.{x|x<-1或x>1} | D.{x|x>1} |