题目内容
函数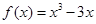 在区间
在区间 上( )
上( )
| A.有最大值,但无最小值 |
| B.有最大值,也有最小值 |
| C.无最大值,但有最小值 |
| D.既无最大值,也无最小值. |
D
解析试题分析: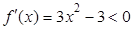 所以
所以 即(-1<x<1)
即(-1<x<1)
所以,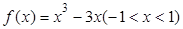 在开区间内单调递减,且不含最值,故答案为:C.
在开区间内单调递减,且不含最值,故答案为:C.
考点:导数研究函数的最值.

练习册系列答案
相关题目
定义在R上的可导函数 f(x)=x2 + 2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,
则m的取值范围是( )
| A.m≥2 | B.2≤m≤4 | C.m≥4 | D.4≤m≤8 |
已知函数f(x)= x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是( )
x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是( )
A.m≥ | B.m> | C.m≤ | D.m< |
函数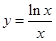 的最大值为( )
的最大值为( )
A. | B. | C.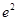 | D. |
函数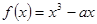 在
在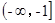 上递增,则
上递增,则 的范围是( )
的范围是( )
A.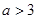 | B.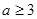 | C. | D.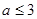 |
[2014·山东济宁]已知f(x)= x2+2xf′(2014)+2014lnx,则f′(2014)=( )
x2+2xf′(2014)+2014lnx,则f′(2014)=( )
| A.2015 | B.-2015 | C.2014 | D.-2014 |
已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( )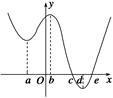
| A.f(b)>f(c)>f(d) |
| B.f(b)>f(a)>f(e) |
| C.f(c)>f(b)>f(a) |
| D.f(c)>f(e)>f(d) |
f(x)=x3﹣3x2+2在区间[﹣1,1]上的最大值是( )
| A.﹣2 | B.0 | C.2 | D.4 |
