Question

【题目】如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC，PA=AB=BC=2．
（1）求证：平面AEF⊥平面PBC；
（2）求三棱锥P﹣AEF的体积．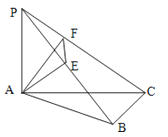

Answer 1

【答案】
解：（1）∵PA⊥平面ABC，BC平面ABC
∴PA⊥BC
又AB⊥BC
∴BC⊥平面PAB，而AE平面PAB
∴BC⊥AE
又AE⊥PB
∴AE⊥平面PBC
而AE平面AEF
∴平面平面AEF⊥平面PBC
（2）由（1）AE⊥平面PBC
又∵AF⊥PC
∴EF⊥PC（三垂线定理逆定理）
∴△PEF∽△PCB
∴
∴S△PEF=S△PBC=
∴VP﹣AEF=VA﹣PEF=××=
【解析】（1）先根据条件得到PA⊥BC进而得BC⊥平面PAB，把问题转化为证AE⊥平面PBC即可；
（2）先根据第一问的结论以及三垂线定理逆定理可得△PEF∽△PCB，求出S△PEF ， 再利用体积相等即可求出结论．
【考点精析】关于本题考查的平面与平面垂直的判定，需要了解一个平面过另一个平面的垂线，则这两个平面垂直才能得出正确答案．