题目内容
3.在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.直线ρsinθ=1与ρ=4sinθ相交所得的弦长为$2\sqrt{3}$.分析 把极坐标方程化为直角坐标方程,把直线方程代入得出交点坐标即可得出.
解答 解:直线ρsinθ=1化为y=1,
ρ=4sinθ化为ρ2=4ρsinθ,可得直角坐标方程:x2+y2=4y,
把y=1代入可得:x2=3,解得x=$±\sqrt{3}$,
因此直线与圆相交所得的弦长为2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了把极坐标方程化为直角坐标方程、直线与圆相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
12.已知$\overrightarrow{a}$=(x,y),$\overrightarrow{b}$=(cosα,sinα),其中x,y,α∈R,若|$\overrightarrow{a}$|=9|$\overrightarrow{b}$|且$\overrightarrow{a}•\overrightarrow{b}$≤λ2+1恒成立,则实数λ的取值范围是( )
| A. | -2$\sqrt{2}$≤λ≤2$\sqrt{2}$ | B. | λ≤-2$\sqrt{2}$或λ≥2$\sqrt{2}$ | C. | λ≥2$\sqrt{2}$ | D. | λ≤-2$\sqrt{2}$ |
 满足约束条件
满足约束条件 ,则
,则 的最小值等于( )
的最小值等于( ) B.-2 C.
B.-2 C. D.2
D.2 中,对所有的正整数
中,对所有的正整数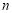 都有
都有 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
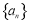 中,
中, ,
, ,则
,则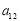 的值是( )
的值是( )