题目内容
20.已知△ABC的三边长分别为5,6,7,点O是△ABC三个角分线的交点,若BC=7,则△OBC的面积为$\frac{7\sqrt{6}}{3}$.分析 由题意和余弦定理求出cosC的值,由平方关系和内角的范围求出sinC的值,代入三角形面积公式求出△ABC的面积,根据三角形角平分线的性质、面积相等点O到BC的距离,再求出△OBC的面积.
解答 解:由题意得,△ABC的三边长分别为5,6,7,且BC=7,
不妨设AB=5,AC=6,
由余弦定理得,cosC=$\frac{A{C}^{2}+B{C}^{2}-A{B}^{2}}{2AC•BC}$=$\frac{36+49-25}{2×6×7}$=$\frac{5}{7}$,
又0<C<π,则sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{2\sqrt{6}}{7}$,
所以△ABC的面积S=$\frac{1}{2}×BC×AC×sinC$=$\frac{1}{2}×7×6×\frac{2\sqrt{6}}{7}$=$6\sqrt{6}$,
因为点O是△ABC三个角分线的交点,所以点O到各个边的距离相等,
设点O到各个边的距离是h,
则△ABC的面积S=$\frac{1}{2}$(5+6+7)h=$6\sqrt{6}$,解得h=$\frac{2\sqrt{6}}{3}$,
所以△OBC的面积S=$\frac{1}{2}×BC×h$=$\frac{1}{2}×$7×$\frac{2\sqrt{6}}{3}$=$\frac{7\sqrt{6}}{3}$
故答案为:$\frac{7\sqrt{6}}{3}$.
点评 本题考查余弦定理,三角函数的平方关系,三角形的面积公式,三角形角平分线的性质,以及等积法的应用,属于中档题.

练习册系列答案
相关题目
12.已知$\overrightarrow{a}$=(x,y),$\overrightarrow{b}$=(cosα,sinα),其中x,y,α∈R,若|$\overrightarrow{a}$|=9|$\overrightarrow{b}$|且$\overrightarrow{a}•\overrightarrow{b}$≤λ2+1恒成立,则实数λ的取值范围是( )
| A. | -2$\sqrt{2}$≤λ≤2$\sqrt{2}$ | B. | λ≤-2$\sqrt{2}$或λ≥2$\sqrt{2}$ | C. | λ≥2$\sqrt{2}$ | D. | λ≤-2$\sqrt{2}$ |
 上的函数
上的函数 满足:①
满足:① ;②
;② ;③当
;③当 时,
时, ,则
,则 、
、 、
、 满足( )
满足( )



 中,对所有的正整数
中,对所有的正整数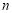 都有
都有 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点.