题目内容

已知函数f(x)＝|lgx|，若0<a<b，且f(a)＝f(b)，则a＋2b的取值范围是________．

 

(3，＋∞)

【解析】因为f(a)＝f(b)，即|lga|＝|lgb|，所以a＝b(舍去)或b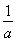＝，得a＋2b＝a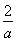＋.又0<a<b，所以0<a<1<b.令f(a)＝a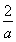＋，则f′(a)＝1－＜0，所以f(a)在a∈(0，1)上为减函数，得f(a)>f(1)＝1＋2＝3，即a＋2b的取值范围是(3，＋∞)．

 

练习册系列答案
相关题目

已知等差数列{an}前三项之和为－3，前三项积为8.

(1)求等差数列{an}的通项公式；

(2)若a2，a3，a1成等比数列，求数列{|an|}的前n项和．

 

若2、a、b、c、9成等差数列，则c－a＝________．

 

若数列中的最大项是第k项，则k＝________．

 

已知函数f(x)＝ax2＋bx(a≠0)的导函数f′(x)＝－2x＋7，数列{an}的前n项和为Sn，点Pn(n，Sn)(n∈N*)均在函数y＝f(x)的图象上，求数列{an}的通项公式及Sn的最大值．

 

已知函数f(x)＝ln＋1，则f(lg2)＋f＝________．

 

(1)设a>1，函数f(x)＝logax在区间[a，2a]上的最大值与最小值之差是，则a＝________；

(2)若a＝log0.40.3，b＝log54，c＝log20.8，用小于号“<”将a、b、c连结起来________；

(3)设f(x)＝lg是奇函数，则使f(x)<0的x的取值范围是________；

(4)已知函数f(x)＝|log2x|，正实数m、n满足m<n且f(m)＝f(n)，若f(x)在区间[m2，n]上的最大值为2，则m、n的值分别为________.

 

已知函数f(x)＝|2x－1－1|.

(1)作出函数y＝f(x)的图象；

(2)若a<c，且f(a)>f(c)，求证：2a＋2c<4.

 

函数f(x)＝(x＋1)(x－a)是偶函数，则f(2)＝________．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网