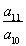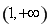题目内容
已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
an=-2n+8(n∈N*),当n=3或n=4时,Sn取得最大值12
【解析】由题意可知:∵f(x)=ax2+bx(a≠0),∴f′(x)=2ax+b,由f′(x)=-2x+7对应相等可得a=-1,b=7,
∴可得f(x)=-x2+7x.因为点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,所以有Sn=-n2+7n.
当n=1时,a1=S1=6;
当n≥2时,an=Sn-Sn-1=-2n+8,a1=6适合上式,
∴an=-2n+8(n∈N*).
令an=-2n+8≥0得n≤4,当n=3或n=4时,Sn取得最大值12.
综上,an=-2n+8(n∈N*),当n=3或n=4时,Sn取得最大值12.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目