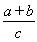Question

已知函数f(x)＝|2x－1－1|.

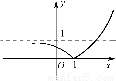
(1)作出函数y＝f(x)的图象；

(2)若a<c，且f(a)>f(c)，求证：2a＋2c<4.

 

Answer 1

（1）

（2）见解析

【解析】(1)f(x)＝其图象如图所示．

(2)证明：由图知，f(x)在(－∞，1]上是减函数，在[1，＋∞)上是增函数，故结合条件知必有a<1.

若c≤1，则2a<2，2c≤2，所以2a＋2c<4；

若c>1，则由f(a)>f(c)，得1－2a－1>2c－1－1，即2c－1＋2a－1<2，所以2a＋2c<4.

综上知，总有2a＋2c<4.