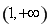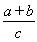题目内容
(1)设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差是 ,则a=________;
,则a=________;
(2)若a=log0.40.3,b=log54,c=log20.8,用小于号“<”将a、b、c连结起来________;
(3)设f(x)=lg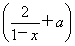 是奇函数,则使f(x)<0的x的取值范围是________;
是奇函数,则使f(x)<0的x的取值范围是________;
(4)已知函数f(x)=|log2x|,正实数m、n满足m<n且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m、n的值分别为________.
(1)4(2)c<b<a(3)-1<x<0(4)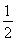 ,2
,2
【解析】
解析:(1)∵a>1,∴函数f(x)=logax在区间[a,2a]上是增函数,∴loga2a-logaa=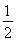 ,∴a=4.
,∴a=4.
(2)由于a>1,0<b<1,c<0,所以c<b<a.
(3)由f(-x)+f(x)=0,得a=-1,则由lg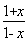 <0,得
<0,得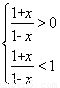 解得-1<x<0.
解得-1<x<0.
(4)结合函数f(x)=|log2x|的图象,易知0<m<1,n>1,且mn=1,所以f(m2)=|log2m2|=2,解得m=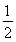 ,所以n=2.
,所以n=2.

练习册系列答案
相关题目