题目内容
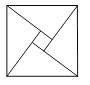
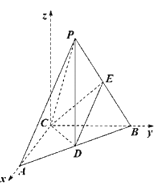
【题目】如图,在三棱锥P-ABC中,AC⊥BC,且,AC=BC=2,D,E分别为AB,PB中点,PD⊥平面ABC,PD=3.
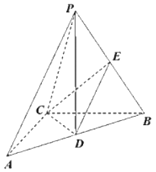
(1)求直线CE与直线PA夹角的余弦值;
(2)求直线PC与平面DEC夹角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)建立空间直角坐标系,确定各点坐标,求出![]() 夹角,即可得结果;
夹角,即可得结果;
(2)求出平面DEC的法向量,其![]() 与法向量夹角的余弦的绝对值,即为所求角的正弦值.
与法向量夹角的余弦的绝对值,即为所求角的正弦值.
建立如图所示的空间直角坐标系,易知C(0,0,0),
A(2,0,0),D(1,1,0),E(![]() ,
,![]() ,
,![]() ),P(1,1,3),
),P(1,1,3),
![]()
设直线CE与直线PA夹角为![]() ,则
,则
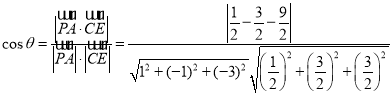
整理得![]() ;
;
![]() 直线CE与直线PA夹角的余弦值
直线CE与直线PA夹角的余弦值![]() ;
;
(2)设直线PC与平面DEC夹角为![]() ,
,
设平面DEC的法向量为![]() ,
,
因为![]() ,
,![]()
所以有
取![]() ,解得
,解得![]() ,
,![]() ,
,
即面DEC的一个法向量为![]() ,
,![]() ,
,
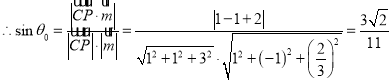 .
.
![]() 直线PC与平面DEC夹角的正弦值为
直线PC与平面DEC夹角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】为庆祝新中国成立七十周年,巴蜀中学将举行“歌唱祖国,喜迎国庆”歌咏比赛活动,《歌唱祖国》,《精忠报国》,《我和我的祖国》等一系列歌曲深受同学们的青睐,高二某班级就该班是否选择《精忠报国》作为本班参赛曲目进行投票表决,投票情况如下表.
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
赞成人数 | 4 | 5 | 6 | 6 | 5 | 6 | 4 | 3 |
总人数 | 7 | 7 | 8 | 8 | 7 | 7 | 6 | 6 |
(1)若从第1小组和第8小组的同学中各随机选取2人进行调查,求所选取的4人中至少有2人赞成《精忠报国》作为本班参赛曲目的概率;
(2)若从第5小组和第7小组的同学中各随机选取2人进行调查,记选取的4人中不赞成《精忠报国》作为本班参赛曲目的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.