题目内容
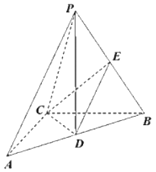
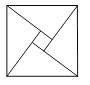
【题目】第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图所示，会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为
，那么
_____________.
【答案】7
【解析】
由已知条件可得每个直角三角形的两条直角边的长度之差为1、斜边的长度为5，设直角三角形的两条直角边分别为a与a+1，勾股定理求出a即可得直角三角形三边长，求出
，代入两角和的正切公式即可得解.
由小正方形的面积为1知每个直角三角形的两条直角边的长度之差为1，
由大正方形的面积为25知每个直角三角形的斜边的长度为5，
设直角三角形的两条直角边分别为a与a+1，
则
，解得
或
(舍去)，
则直角三角形的两条直角边为3、4，斜边为5，
所以
，
.
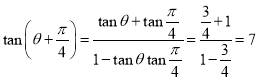故答案为：7
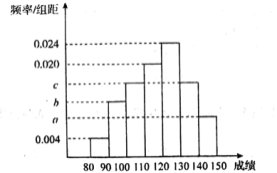
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示，成绩分组区间为：
.其中a，b，c成等差数列且
.物理成绩统计如表.（说明：数学满分150分，物理满分100分）
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
（1）根据频率分布直方图，请估计数学成绩的平均分；
（2）根据物理成绩统计表，请估计物理成绩的中位数；
（3）若数学成绩不低于140分的为“优”，物理成绩不低于90分的为“优”，已知本班中至少有一个“优”同学总数为6人，从此6人中随机抽取3人，记X为抽到两个“优”的学生人数，求X的分布列和期望值.
【题目】为了增强消防意识，某部门从男职工中随机抽取了50人，从女职工中随机抽取了40人参加消防知识测试，按优秀程度制作了如下
列联表：
优秀 | 非优秀 | 总计 | |
男职工 | 35 | ||
女职工 | |||
总计 | 50 |
（1）完成列联表；
（2）判断是否有
的把握认为消防知识是否优秀与性别有关.
附：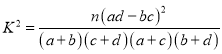
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】在测试中，客观题难度的计算公式为
，其中
为第
题的难度，
为答对该题的人数，
为参加测试的总人数.现对某校高三年级240名学生进行一次测试，共5道客观题.测试前根据对学生的了解，预估了每道题的难度，如下表所示：
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后，随机抽取了20名学生的答题数据进行统计，结果如下：
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | 16 | 16 | 14 | 14 | 8 |
