题目内容
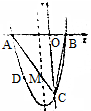
13.已知椭圆x2+2y2=1,过原点的两条直线l1和l2分别与椭圆交于点A、B和C、D,记△AOC的面积为S.(1)设A(x1,y1),C(x2,y2),用A、C的坐标表示点C到直线l1的距离,并证明S=$\frac{1}{2}|{{x_1}{y_2}-{x_2}{y_1}}$|;
(2)设l1:y=kx,$C({\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$,S=$\frac{1}{3}$,求k的值;
(3)设l1与l2的斜率之积为m,求m的值,使得无论l1和l2如何变动,面积S保持不变.
分析 (1)依题意,直线l1的方程为y=$\frac{{y}_{1}}{{x}_{1}}$x,利用点到直线间的距离公式可求得点C到直线l1的距离d=$\frac{|{y}_{1}{x}_{2}-{x}_{1}{y}_{2}|}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}}$,再利用|AB|=2|AO|=2$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$,可证得S=$\frac{1}{4}$|AB|d=$\frac{1}{2}$|x1y2-x2y1|;
(2)由(1)得:S=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$|x1-y1|=$\frac{1}{3}$,进而得到答案;
(3)方法一:设直线l1的斜率为k,则直线l1的方程为y=kx,联立方程组$\left\{\begin{array}{l}y=kx\\{x}^{2}+2{y}^{2}=1\end{array}\right.$,消去y解得x=±$\frac{1}{\sqrt{1+2{k}^{2}}}$,可求得x1、x2、y1、y2,利用S=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$•$\frac{|m-{k}^{2}|}{\sqrt{(1+2{k}^{2}{)(k}^{2}+2{m}^{2})}}$,设$\frac{|m-{k}^{2}|}{\sqrt{(1+2{k}^{2}){(k}^{2}+2{m}^{2})}}$=c(常数),整理得:k4-2mk2+m2=c2[2k4+(1+4m2)k2+2m2],由于左右两边恒成立,可得$\left\{\begin{array}{l}{c}^{2}=\frac{1}{2}\\ m=-\frac{1}{2}\end{array}\right.$,此时S=$\frac{\sqrt{2}}{4}$;
方法二:设直线l1、l2的斜率分别为$\frac{{y}_{1}}{{x}_{1}}$、$\frac{{y}_{2}}{{x}_{2}}$,则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=m,则mx1x2=-y1y2,变形整理,利用A(x1,y1)、C(x2,y2)在椭圆x2+2y2=1上,可求得面积S的值.
解答 解:(1)依题意,直线l1的方程为y=$\frac{{y}_{1}}{{x}_{1}}$x,由点到直线间的距离公式得:点C到直线l1的距离d=$\frac{|\frac{{y}_{1}{x}_{2}}{{x}_{1}}-{y}_{2}|}{\sqrt{1+{(\frac{{y}_{1}}{{x}_{1}})}^{2}}}$=$\frac{|{y}_{1}{x}_{2}-{x}_{1}{y}_{2}|}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}}$,
因为|AB|=2|AO|=2$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$,所以S=$\frac{1}{4}$|AB|d=$\frac{1}{2}$|x1y2-x2y1|;
(2)由(1)A(x1,y1),C(x2,y2),
S=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$|x1-y1|=$\frac{1}{3}$.
所以|x1-y1|=$\frac{2\sqrt{3}}{3}$,由x12+2y12=1,
解得A($\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$)或($\frac{5\sqrt{3}}{9}$,-$\frac{\sqrt{3}}{9}$)
或(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$)或(-$\frac{5\sqrt{3}}{9}$,$\frac{\sqrt{3}}{9}$),
由k=$\frac{{y}_{1}}{{x}_{1}}$,得k=-1或-$\frac{1}{5}$;
(3)方法一:设直线l1的斜率为k,则直线l2的斜率为$\frac{m}{k}$,直线l1的方程为y=kx,
联立方程组$\left\{\begin{array}{l}y=kx\\{x}^{2}+2{y}^{2}=1\end{array}\right.$,消去y解得x=±$\frac{1}{\sqrt{1+2{k}^{2}}}$,
根据对称性,设x1=$\frac{1}{\sqrt{1+2{k}^{2}}}$,则y1=$\frac{k}{\sqrt{1+2{k}^{2}}}$,
同理可得x2=$\frac{k}{\sqrt{{k}^{2}+2{m}^{2}}}$,y2=$\frac{m}{\sqrt{{k}^{2}+2{m}^{2}}}$,
所以S=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$•$\frac{|m-{k}^{2}|}{\sqrt{(1+2{k}^{2}{)(k}^{2}+2{m}^{2})}}$,设$\frac{|m-{k}^{2}|}{\sqrt{(1+2{k}^{2}){(k}^{2}+2{m}^{2})}}$=c(常数),
所以(m-k2)2=c2(1+2k2)(k2+2m2),
整理得:k4-2mk2+m2=c2[2k4+(1+4m2)k2+2m2],
由于左右两边恒成立,所以只能是$\left\{\begin{array}{l}2{c}^{2}=1\\{c}^{2}(1+4{m}^{2})=-2m\end{array}\right.$,所以$\left\{\begin{array}{l}{c}^{2}=\frac{1}{2}\\ m=-\frac{1}{2}\end{array}\right.$,此时S=$\frac{\sqrt{2}}{4}$,
综上所述,m=-$\frac{1}{2}$,S=$\frac{\sqrt{2}}{4}$.
方法二:设直线l1、l2的斜率分别为$\frac{{y}_{1}}{{x}_{1}}$、$\frac{{y}_{2}}{{x}_{2}}$,则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=m,
所以mx1x2=y1y2,
∴m2${{x}_{1}}^{2}{{x}_{2}}^{2}$=${{y}_{1}}^{2}{{y}_{2}}^{2}$=mx1x2y1y2,
∵A(x1,y1)、C(x2,y2)在椭圆x2+2y2=1上,
∴(${{x}_{1}}^{2}{{+2y}_{1}}^{2}$)(${{x}_{2}}^{2}{{+2y}_{2}}^{2}$)=${{x}_{1}}^{2}{{x}_{2}}^{2}$+4${{y}_{1}}^{2}{{y}_{2}}^{2}$+2(${{x}_{1}}^{2}{{y}_{2}}^{2}$+${{x}_{2}}^{2}{{y}_{1}}^{2}$)=1,
即($\frac{1}{m}$+4m)x1x2y1y2+2(${{x}_{1}}^{2}{{y}_{2}}^{2}$+${{x}_{2}}^{2}{{y}_{1}}^{2}$)=1,
所以${{x}_{1}}^{2}{{y}_{2}}^{2}$+${{x}_{2}}^{2}{{y}_{1}}^{2}$-2x1x2y1y2=(x1y2-x2y1)2=$\frac{1}{2}$[1-(4m+$\frac{1}{m}$)x1x2y1y2]-2x1x2y1y2
=$\frac{1}{2}$-(2m+$\frac{1}{2m}$+2)x1x2y1y2,是常数,所以|x1y2-x2y1|是常数,
所以令2m+$\frac{1}{2m}$+2=0即可,
所以,m=-$\frac{1}{2}$,S=$\frac{\sqrt{2}}{4}$.
综上所述,m=-$\frac{1}{2}$,S=$\frac{\sqrt{2}}{4}$.
点评 本题考查直线与圆锥曲线的综合应用,考查方程思想、等价转化思想与综合运算能力,属于难题.