题目内容
9.已知函数f(x)=lnx+a|x2-1|(a∈R).(1)当a=1时,求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在(0,$\sqrt{e}$)上的最大值g(a).
分析 (1)得出当a=1时,f(x)=lnx+|x2-1|=$\left\{\begin{array}{l}{lnx+{x}^{2}-1,x≥1}\\{lnx+1-{x}^{2},0<x<1}\end{array}\right.$分段求解导数判断即可.
(2)去绝对值得出:当a>0时,f(x)=$\left\{\begin{array}{l}{lnx+a{x}^{2}-a,x≥1}\\{lnx+a-a{x}^{2},0<x<1}\end{array}\right.$,
利用导数分类讨论得出:当0<a$≤\frac{1}{2}$时,f(x)在(0,$\sqrt{e}$)上单调递增,f(x)无最大值,
当a$>\frac{1}{2}$时,f(x)在(0,$\frac{\sqrt{2a}}{2a}$)上单调递增,($\frac{\sqrt{2a}}{2a}$,1)单调递减,在(1,$\sqrt{e}$)上单调递增,
极大值为f($\frac{\sqrt{2a}}{2a}$),极小值为f(1).
比较f($\sqrt{e}$)>f($\frac{\sqrt{2a}}{2a}$),即可判断最值情况.
解答 解:∵f(x)=lnx+a|x2-1|(a∈R).
∴(1)当a=1时,f(x)=lnx+|x2-1|=$\left\{\begin{array}{l}{lnx+{x}^{2}-1,x≥1}\\{lnx+1-{x}^{2},0<x<1}\end{array}\right.$
∵当x≥1时,f′(x)=$\frac{1}{x}$+2x>0,
∴函数f(x)在(1,+∞)上单调递增,
∵当0<x<1时,f′(x)=$\frac{1}{x}$-2x=$\frac{1-2{x}^{2}}{x}$,
1-2x2>0,0<x$<\frac{\sqrt{2}}{2}$
1-2x2<0,x$>\frac{\sqrt{2}}{2}$,
∴函数f(x)在(0,$\frac{\sqrt{2}}{2}$)上单调递增,在($\frac{\sqrt{2}}{2}$,1)上单调递减,
(2)函数f(x)=lnx+a|x2-1|(a∈R).
当a>0时,f(x)=$\left\{\begin{array}{l}{lnx+a{x}^{2}-a,x≥1}\\{lnx+a-a{x}^{2},0<x<1}\end{array}\right.$
①∵当x≥1时,f′(x)=$\frac{1}{x}$+2ax>0,
∴函数f(x)在(1,+∞)上单调递增,
②∵当0<x<1时,f′(x)=$\frac{1}{x}$-2ax=$\frac{1-2a{x}^{2}}{x}$,
1-2ax2>0,0<x$<\frac{\sqrt{2a}}{2a}$
1-2ax2<0,x$>\frac{\sqrt{2a}}{2a}$,
∴当0<a$≤\frac{1}{2}$时,$\frac{\sqrt{2a}}{2a}$≥1,f(x)在(0,1)上单调递增,
当a$>\frac{1}{2}$时,0<$\frac{\sqrt{2a}}{2a}$<1,f(x)在(0,$\frac{\sqrt{2a}}{2a}$)上单调递增,($\frac{\sqrt{2a}}{2a}$,1)单调递减,
综上:当0<a$≤\frac{1}{2}$时,f(x)在(0,$\sqrt{e}$)上单调递增,f(x)无最大值,
当a$>\frac{1}{2}$时,f(x)在(0,$\frac{\sqrt{2a}}{2a}$)上单调递增,($\frac{\sqrt{2a}}{2a}$,1)单调递减,在(1,$\sqrt{e}$)上单调递增,
极大值为f($\frac{\sqrt{2a}}{2a}$),极小值为f(1).
f($\frac{\sqrt{2a}}{2a}$)=ln$\frac{\sqrt{2a}}{2a}$+a|$\frac{1}{2a}$-1|=ln$\frac{\sqrt{2a}}{2a}$+|$\frac{1}{2}-a$|=ln$\frac{\sqrt{2a}}{2a}$$+a-\frac{1}{2}$$<a-\frac{1}{2}$
f($\sqrt{e}$)=$\frac{1}{2}$+a|e-1|=$\frac{1}{2}+ae-a$,
∵$\frac{1}{2}+ae-a$-(a-$\frac{1}{2}$)=ae-2a+1=a(e-2)+1>0,
∴f($\sqrt{e}$)>f($\frac{\sqrt{2a}}{2a}$)
∴在(0,$\sqrt{e}$)f(x)无最大值,
∴当a>0时,求函数f(x)在(0,$\sqrt{e}$)上无最大值.
点评 本题综合考查了导数在求解函数单调性,最值中的应用,分类讨论,求解不等式,中和性较大,属于难度较大的题目.

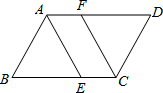 如图所示,平行四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,根据现有的图形请添加一个条件,使四边形AECF是菱形,则添加的一个条件可以是AC⊥EF(只写出一个即可)
如图所示,平行四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,根据现有的图形请添加一个条件,使四边形AECF是菱形,则添加的一个条件可以是AC⊥EF(只写出一个即可)