题目内容
如图,已知椭圆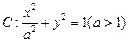 的上顶点为
的上顶点为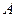 ,右焦点为
,右焦点为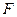 ,直线
,直线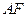 与圆
与圆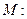
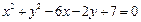 相切.
相切.
(Ⅰ)求椭圆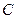 的方程;
的方程;
(Ⅱ)若不过点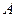 的动直线
的动直线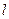 与椭圆
与椭圆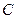 相交于
相交于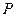 、
、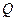 两点,且
两点,且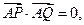 求证:直线
求证:直线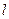 过定点,并求出该定点
过定点,并求出该定点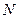 的坐标.
的坐标.

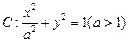 的上顶点为
的上顶点为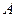 ,右焦点为
,右焦点为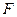 ,直线
,直线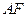 与圆
与圆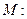
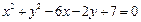 相切.
相切.(Ⅰ)求椭圆
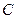 的方程;
的方程;(Ⅱ)若不过点
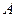 的动直线
的动直线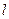 与椭圆
与椭圆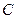 相交于
相交于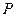 、
、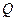 两点,且
两点,且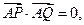 求证:直线
求证:直线 过定点,并求出该定点
过定点,并求出该定点 的坐标.
的坐标.
(Ⅰ)将圆 的一般方程
的一般方程 化为标准方程
化为标准方程
 ,圆
,圆 的圆心为
的圆心为 ,半径
,半径 .
.
由 ,
, 得直线
得直线 ,
,
即 ,
,
由直线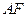 与圆
与圆 相切,得
相切,得 ,
,

 或
或 (舍去). -----------------------------------2分
(舍去). -----------------------------------2分
当 时,
时,  ,
,
故椭圆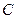 的方程为
的方程为 ---------------------------------4分
---------------------------------4分
(Ⅱ)(方法一)由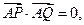 知
知 ,从而直线
,从而直线 与坐标轴不垂直,
与坐标轴不垂直,
由 可设直线
可设直线 的方程为
的方程为 ,
,
直线 的方程为
的方程为 .
.
将 代入椭圆
代入椭圆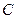 的方程
的方程
并整理得: ,-----------------------------------6分
,-----------------------------------6分
解得 或
或 ,因此
,因此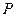 的坐标为
的坐标为 ,
,
即 ------------------------------------------8分
------------------------------------------8分
将上式中的 换成
换成 ,得
,得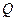
 .
.
直线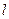 的方程为
的方程为
化简得直线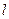 的方程为
的方程为 ,
,
因此直线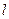 过定点
过定点 .
.
 的一般方程
的一般方程 化为标准方程
化为标准方程  ,圆
,圆 的圆心为
的圆心为 ,半径
,半径 .
. 由
 ,
, 得直线
得直线 ,
,即
 ,
, 由直线
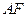 与圆
与圆 相切,得
相切,得 ,
, 
 或
或 (舍去). -----------------------------------2分
(舍去). -----------------------------------2分 当
 时,
时,  ,
, 故椭圆
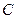 的方程为
的方程为 ---------------------------------4分
---------------------------------4分(Ⅱ)(方法一)由
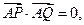 知
知 ,从而直线
,从而直线 与坐标轴不垂直,
与坐标轴不垂直,由
 可设直线
可设直线 的方程为
的方程为 ,
,直线
 的方程为
的方程为 .
. 将
 代入椭圆
代入椭圆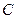 的方程
的方程
并整理得:
 ,-----------------------------------6分
,-----------------------------------6分解得
 或
或 ,因此
,因此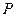 的坐标为
的坐标为 ,
,即
 ------------------------------------------8分
------------------------------------------8分 将上式中的
 换成
换成 ,得
,得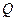
 .
. 直线
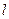 的方程为
的方程为
化简得直线
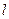 的方程为
的方程为 ,
, 因此直线
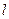 过定点
过定点 .
.略

练习册系列答案
相关题目
 出发,经过直线
出发,经过直线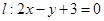 上的一点D反射后,经过点
上的一点D反射后,经过点 .
.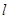 交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。
交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。 与椭圆交于A,B两点,
与椭圆交于A,B两点, 的面积为4,
的面积为4, 的周长为
的周长为 (I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
(I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。 焦点在
焦点在 轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P.
 与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q(
与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q( ,0),求
,0),求 的最小值.
的最小值. 与椭圆
与椭圆 相交于A、B两点.
相交于A、B两点. ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长; 与向量
与向量 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率 时,求椭圆的长轴长的最大值
时,求椭圆的长轴长的最大值 的焦点恰好是椭圆
的焦点恰好是椭圆 的右焦点
的右焦点 ,且两条曲线的交点连线也过焦点
,且两条曲线的交点连线也过焦点

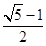

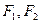 是椭圆
是椭圆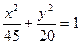 的两个焦点,
的两个焦点,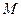 是椭圆上的点,且
是椭圆上的点,且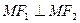 .
.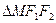 的周长;
的周长;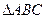 的两个顶点
的两个顶点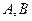 的坐标分别为
的坐标分别为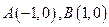 ,平面内两点
,平面内两点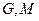 同时满足一下条件:①
同时满足一下条件:①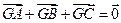 ;②
;②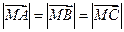 ;③
;③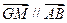
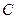 的轨迹方程;
的轨迹方程;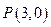 的直线
的直线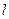 与(1)中的轨迹交于
与(1)中的轨迹交于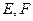 两点,求
两点,求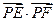 的取值范围。
的取值范围。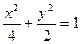 的左、右焦点分别为
的左、右焦点分别为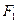 、
、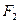 ,直线
,直线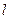 过
过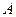 、
、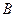 两点,
两点,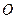 为坐标原点,以
为坐标原点,以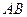 为直径的圆恰好过
为直径的圆恰好过