题目内容
已知函数 。
。
(1)求函数 的定义域;
的定义域;
(2)判断函数 的奇偶性;
的奇偶性;
(3)讨论函数 的单调性(不用证明)。
的单调性(不用证明)。
(1) ;(2)奇函数;(3)
;(2)奇函数;(3)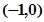 减函数 ;
减函数 ; 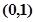 减函数;
减函数;
解析试题分析:(1)由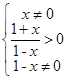 得:
得: ,所以函数的定义域为
,所以函数的定义域为 。
。
(2)由(1)知,函数的定义域为 ,关于原点对称,
,关于原点对称,
又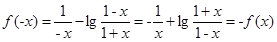 ,所以f(x) 是奇函数。
,所以f(x) 是奇函数。
(3)令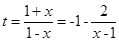 ,则函数t在(0,1)上是单调递增的,又y=-lgt在(0,1)上是单调递减的,所以y=
,则函数t在(0,1)上是单调递增的,又y=-lgt在(0,1)上是单调递减的,所以y= 在(0,1)上是单调递减的,所以
在(0,1)上是单调递减的,所以 在(0,1)上是单调递减的,,又因为f(x)是奇函数,所以f(x) 在(-1,0)上是单调递减的。
在(0,1)上是单调递减的,,又因为f(x)是奇函数,所以f(x) 在(-1,0)上是单调递减的。
考点:本题考查函数的定义域;函数的奇偶性;函数的单调性;分式不等式的解法;复合函数的单调性。
点评:本题主要考查了奇偶性与单调性的综合,同时也考查了函数的定义域,复合函数等。熟练掌握基本初等函数的性质和复合函数单调性的判断是解答本题的关键.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 ,
, .
. (其中
(其中 是
是 的导函数),求
的导函数),求 的最大值;
的最大值; 时,有
时,有 ;
; ,当
,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的最大值.
的最大值.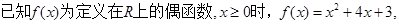
 时函数的解析式
时函数的解析式 上是单调递增
上是单调递增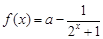 ,
,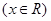 .
. 为何实数
为何实数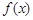 在
在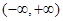 上为增函数;
上为增函数;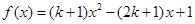 ,
, .
.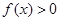 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,
时, 恒成立,求实数
恒成立,求实数 时,解不等式
时,解不等式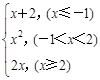 .
.
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求: 的根为一正一负,则求实数
的根为一正一负,则求实数 内,则求实数
内,则求实数 ,
, 是
是 的一个极值点.
的一个极值点.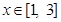 时,
时,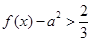 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的函数
的函数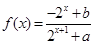 是奇函数
是奇函数  的解析式;
的解析式;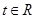 ,不等式
,不等式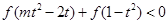 恒成立,求
恒成立,求 的取值范围.
的取值范围.