题目内容

6．当0＜k＜1时，函数f（x）=|1-x2|-（kx-k）零点个数是（　　）
A．4B．3C．2D．1

分析 由题意设y=|1-x2|、y=k（x-1），由k的范围在同一个坐标系中画出两个函数的图象，根据图象的交点个数可得到答案．

解答 解：由题意设y=|1-x2|，y=k（x-1）其中0＜k＜1，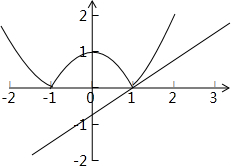
在同一个坐标系中画出两个函数的图象：
由图可得：y=|1-x2|与y=k（x-1）的图象有1个交点，
所以函数f（x）=|1-x2|-（kx-k）零点个数是1，
故选：D．

点评 本题考查函数零点的问题转化为两个图象的交点问题，考查转化思想、数形结合思想，属于中档题．

练习册系列答案
相关题目
13．将正奇数排列如下表其中第i行第j个数表示aij（i∈N*，j∈N*），如a32=9，若aij=2011，则i+j=61．
17．在平面直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=t+\sqrt{3}m}\\{y=-\sqrt{3}t-2m}\end{array}\right.$（t为参数），若以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ（1-cos2θ）=8cosθ
（1）求曲线C的直角坐标方程；
（2）若直线l与曲线C相切，求直线l与坐标轴围成的三角形的面积．
14．设函数f（x）=|x-1|+|x+2|
（1）解不等式f（x）≥5；
（2）对任意x∈R，f（x）≥a2-2a都成立，求实数a的范围．
1．已知函数f（x）=-$\sqrt{3}$sin2x+sinxcosx．
（1）求f（$\frac{13}{6}$π）的值；
（2）设α∈（0，π），f（$\frac{α}{2}$）=$\frac{1}{4}$-$\frac{\sqrt{3}}{2}$，求sinα的值．
11．如果a＜3，则下列结论一定正确的是（　　）
A．a2＞9B．a2＜9C．a3＞27D．a3＜27
18．下列求导运算正确的是（　　）
A．[（3-x2）（1+x）]′=3x2-2x+6B．（sinx-cosx）′=cosx-sinx
C．$（x\sqrt{x}-{e^x}）'=\frac{3}{2}x-{e^x}$D．$（\frac{1-x}{1+x}）'=-\frac{2}{{{{（1+x）}^2}}}$
15．已知函数f（x）=|x-m|，关于x的不等式f（x）≤3的解集为[-1，5]
（Ⅰ）求实数m的值；
（Ⅱ）若实数a、b、c满足a-2b+c=m，求a2+b2+c2的最小值．
16．若函数f（x）=x3-a的图象不经过第二象限，则实数a的取值范围是[0，+∞）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网