题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 的最小值为
的最小值为![]() ,且该椭圆的离心率为
,且该椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 上不同的两点,且
上不同的两点,且![]() ,若
,若![]() ,试问直线
,试问直线![]() 是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
【答案】(1)![]() (2)直线
(2)直线![]() 过定点
过定点![]()
【解析】
(1)依题意得到方程组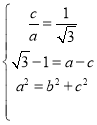 解得;
解得;
(2)已知![]() 且
且![]() ,可知点
,可知点![]() 同在
同在![]() 轴的上方或下方,
轴的上方或下方,
由对称性可知,若动直线![]() 经过一个定点,则该定点在
经过一个定点,则该定点在![]() 轴上,因为
轴上,因为![]() ,所以点
,所以点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程,列出韦达定理,由直线
,联立直线与椭圆方程,列出韦达定理,由直线![]() 的斜率
的斜率![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,令
,令![]() ,计算其横坐标是否为定值.
,计算其横坐标是否为定值.
解:(1)依题意得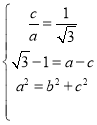 ,解得
,解得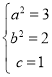 ,所以椭圆
,所以椭圆![]() ;
;
(2)直线![]() 过定点
过定点![]() ,
,
证明:已知![]() 且
且![]() ,可知点
,可知点![]() 同在
同在![]() 轴的上方或下方,
轴的上方或下方,
由对称性可知,若动直线![]() 经过一个定点,则该定点在
经过一个定点,则该定点在![]() 轴上,
轴上,
因为![]() ,所以点
,所以点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立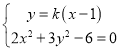 ,消去
,消去![]() 整理得
整理得![]() 又
又![]() ,
,
所以 ,
,
由直线![]() 的斜率
的斜率![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得:
,得:![]() ,
,
由![]() ,
,
所以![]()
即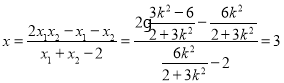 ,
,
所以直线![]() 过定点
过定点![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】为研究女高中生身高与体重之间的关系,一调查机构从某中学中随机选取8名女高中生,其身高![]() 和体重
和体重![]() 数据如下表所示:
数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 164 | 160 | 158 | 172 | 162 | 164 | 174 | 166 |
体重 | 60 | 46 | 43 | 48 | 48 | 50 | 61 | 52 |
该调查机构绘制出该组数据的散点图后分析发现,女高中生的身高与体重之间有较强的线性相关关系.

(1)调查员甲计算得出该组数据的线性回归方程为![]() ,请你据此预报一名身高为
,请你据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(2)调查员乙仔细观察散点图发现,这8名同学中,编号为1和4的两名同学对应的点与其他同学对应的点偏差太大,于是提出这样的数据应剔除,请你按照这名调查人员的想法重新计算线性回归话中,并据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(3)请你分析一下,甲和乙谁的模型得到的预测值更可靠?说明理由.
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: .
.