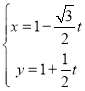Question

【题目】如图，在极坐标系中，曲线C1是以C1（4，0）为圆心的半圆，曲线C2是以为圆心的圆，曲线C1、C2都过极点O．

（1）分别写出半圆C1，C2的极坐标方程；

（2）直线l：与曲线C1，C2分别交于M、N两点（异于极点O），P为C2上的动点，求△PMN面积的最大值．

Answer 1

【答案】（1）；；（2）．

【解析】

（1）直接利用转换关系的应用，把参数方程极坐标方程和直角坐标方程之间进行转换．

（2）利用三角函数关系式的变换和三角形的面积的公式的应用求出结果．

（1）曲线C1是以C1（4，0）为圆心的半圆，

所以半圆的极坐标方程为，

曲线C2是以为圆心的圆，转换为极坐标方程为．

（2）由（1）得：|MN|＝|．

显然当点P到直线MN的距离最大时，△PMN的面积最大．

此时点P为过C2且与直线MN垂直的直线与C2的一个交点，

设PC2与直线MN垂直于点H，

如图所示：

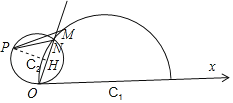
在Rt△OHC2中，|，

所以点P到直线MN的最大距离d，

所以．