��Ŀ����
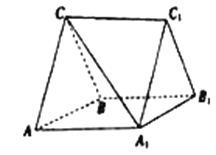
����Ŀ����ͼ��Ϊ�������Ϲ���OA���滮��һ������BC��ͬʱ����һ��Բ�α��������滮Ҫ������BC��Ӱ�AB��ֱ���������ı߽�ΪԲ��M���߶�OA�ϲ���BC���е�Բ���ҹ�������O��A����Բ������һ��ľ����������80m������������Aλ�ڵ�O��������60m������Cλ�ڵ�O��������170m����OCΪ�Ӱ�����tan��BCO= ![]() ��
�� 
��1��������BC�ij���
��2����OM�ʱ��Բ�α�������������
���𰸡�
��1���⣺��ͼ��

��B��BE��OC��E����A��AF��BE��F��
�ߡ�ABC=90�㣬��BEC=90�㣬
���ABF=��BCE��
�� ![]() ��
��
��AF=4x��m������BF=3x��m����
�ߡ�AOE=��AFE=��OEF=90�㣬
��OE=AF=4x��m����EF=AO=60��m����
��BE=��3x+60��m��
�� ![]() ��
��
��CE= ![]() ��m����
��m����
�� ![]() ��m����
��m����
�� ![]() ��
��
��ã�x=20��
��BE=120m��CE=90m��
��BC=150m
��2���⣺��ͼ��

��BC���M����Q���ӳ�QM��CO����P��
�ߡ�POM=��PQC=90�㣬
���PMO=��BCO��
��OM=xm����OP= ![]() m��PM=
m��PM= ![]() m��
m��
��PC= ![]() m��PQ=
m��PQ= ![]() m��
m��
���M�뾶ΪR��
��R=MQ= ![]() m=
m= ![]() m��
m��
��A��O����M����һ����벻����80m��
��R��AM��80��R��OM��80��
��136�� ![]() ����60��x����80��136��
����60��x����80��136�� ![]() ��x��80��
��x��80��
��ã�10��x��35��
�൱�ҽ���x=10ʱRȡ�����ֵ��
��OM=10mʱ��������������
����������1�����ı���AOCB�У���B��BE��OC��E����A��AF��BE��F�����AF��Ȼ��ͨ����ֱ����������ʽ���BE����һ���õ�CE��Ȼ���ɹ��ɶ����ô𰸣���2����BC���M����Q���ӳ�QM��CO����P����OM=xm����PC��PQ�ú���x�Ĵ���ʽ��ʾ���ٽ�Ϲ�������O��A����Բ������һ��ľ����������80m��ʽ���x�ķ�Χ���õ�xȡ��СֵʱԲ�İ뾶���Բ�α�������������

 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д�