题目内容
(本小题满分13分)
已知抛物线 :
: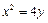 的焦点为
的焦点为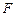
 ,过点
,过点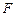 作直线
作直线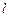 交抛物线
交抛物线 于
于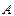 、
、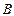 两点;椭圆
两点;椭圆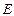 的中心在原点,焦点在
的中心在原点,焦点在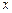 轴上,点
轴上,点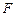 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率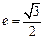 .
.
(1)求椭圆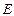 的方程;
的方程;
(2)经过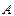 、
、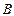 两点分别作抛物线
两点分别作抛物线 的切线
的切线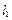 、
、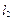 ,切线
,切线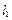 与
与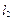 相交于点
相交于点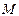 .证明:
.证明: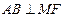 ;
;
(3)椭圆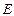 上是否存在一点
上是否存在一点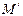 ,经过点
,经过点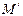 作抛物线
作抛物线 的两条切线
的两条切线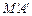 、
、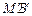 (
(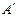 、
、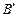 为切点),使得直线
为切点),使得直线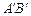 过点
过点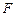 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线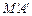 、
、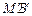 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由.
已知抛物线
 :
: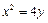 的焦点为
的焦点为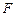
 ,过点
,过点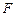 作直线
作直线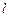 交抛物线
交抛物线 于
于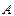 、
、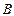 两点;椭圆
两点;椭圆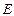 的中心在原点,焦点在
的中心在原点,焦点在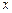 轴上,点
轴上,点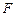 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率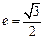 .
.(1)求椭圆
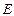 的方程;
的方程;(2)经过
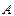 、
、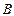 两点分别作抛物线
两点分别作抛物线 的切线
的切线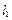 、
、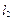 ,切线
,切线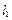 与
与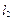 相交于点
相交于点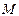 .证明:
.证明: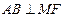 ;
;(3)椭圆
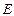 上是否存在一点
上是否存在一点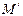 ,经过点
,经过点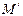 作抛物线
作抛物线 的两条切线
的两条切线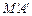 、
、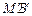 (
(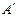 、
、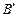 为切点),使得直线
为切点),使得直线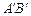 过点
过点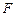 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线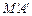 、
、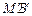 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由.
|
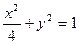
(2)略
(3)椭圆
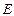 上存在一点
上存在一点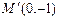 ,经过点
,经过点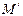 作抛物线
作抛物线 的两条切线
的两条切线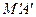 、
、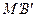 (
(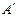 、
、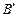 为切点),能使直线
为切点),能使直线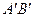 过点
过点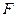 .
.此时,两切线的方程分别为
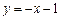 和
和 . …………11分
. …………11分抛物线
 与切线
与切线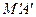 、
、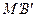 所围成图形的面积为
所围成图形的面积为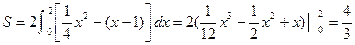
解:(1)设椭圆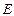 的方程为
的方程为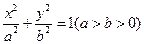 ,半焦距为
,半焦距为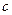 .
.
由已知条件,得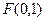 ,
,
∴
解得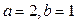 .
.
所以椭圆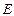 的方程为:
的方程为: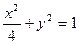 . …………
. …………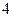 分
分
(2)显然直线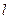 的斜率存在,否则直线
的斜率存在,否则直线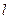 与抛物线
与抛物线 只有一个交点,不合题意,
只有一个交点,不合题意,
故可设直线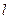 的方程为
的方程为 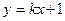 ,
,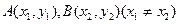 ,
,
由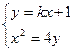
消去 并整理得
并整理得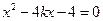 ,
,
∴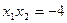 . …………
. …………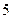 分
分
∵抛物线 的方程为
的方程为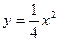 ,求导得
,求导得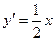 ,
,
∴过抛物线 上
上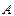 、
、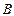 两点的切线方程分别是
两点的切线方程分别是
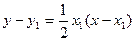 ,
, 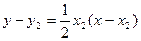 ,
,
即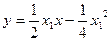 ,
, 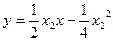 ,
,
解得两条切线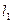 、
、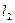 的交点
的交点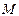 的坐标为
的坐标为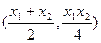 ,即
,即 ,……
,……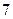 分
分
∴


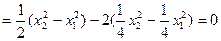
∴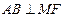 .
.  …………8分
…………8分
(3)假设存在点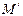 满足题意,由(2)知点
满足题意,由(2)知点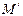 必在直线
必在直线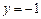 上,又直线
上,又直线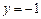 与椭圆
与椭圆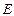 有唯一交点,故
有唯一交点,故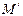 的坐标为
的坐标为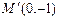 ,
,
设过点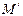 且与抛物线
且与抛物线 相切的切线方程为:
相切的切线方程为: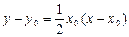 ,其中点
,其中点 为切点.
为切点.
令 得,
得,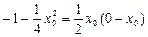 ,
,
解得 或
或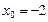 , ………
, ……… …10分
…10分
故不妨取 ,即直线
,即直线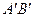 过点
过点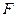 .
.
综上所述,椭圆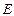 上存在一点
上存在一点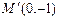 ,经过点
,经过点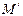 作抛物线
作抛物线 的两条切线
的两条切线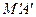 、
、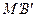 (
(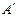 、
、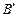 为切点),能使直线
为切点),能使直线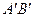 过点
过点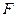 .
.
此时,两切线的方程分别为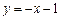 和
和 . …………11分
. …………11分
抛物线 与切线
与切线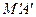 、
、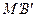 所围成图形的面积为
所围成图形的面积为
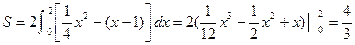 . …………13分
. …………13分
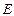 的方程为
的方程为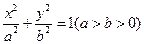 ,半焦距为
,半焦距为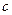 .
.由已知条件,得
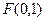 ,
,∴

解得
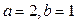 .
.所以椭圆
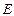 的方程为:
的方程为: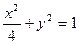 . …………
. …………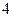 分
分(2)显然直线
 的斜率存在,否则直线
的斜率存在,否则直线 与抛物线
与抛物线 只有一个交点,不合题意,
只有一个交点,不合题意,故可设直线
 的方程为
的方程为 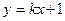 ,
,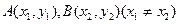 ,
,由
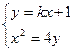
消去
 并整理得
并整理得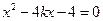 ,
,∴
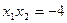 . …………
. …………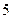 分
分∵抛物线
 的方程为
的方程为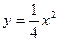 ,求导得
,求导得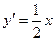 ,
,∴过抛物线
 上
上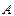 、
、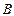 两点的切线方程分别是
两点的切线方程分别是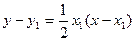 ,
, 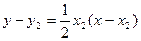 ,
,即
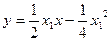 ,
, 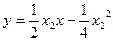 ,
,解得两条切线
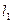 、
、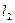 的交点
的交点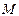 的坐标为
的坐标为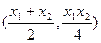 ,即
,即 ,……
,……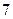 分
分∴



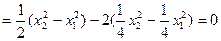
∴
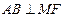 .
.  …………8分
…………8分(3)假设存在点
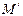 满足题意,由(2)知点
满足题意,由(2)知点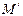 必在直线
必在直线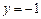 上,又直线
上,又直线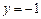 与椭圆
与椭圆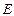 有唯一交点,故
有唯一交点,故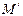 的坐标为
的坐标为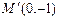 ,
,设过点
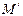 且与抛物线
且与抛物线 相切的切线方程为:
相切的切线方程为: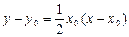 ,其中点
,其中点 为切点.
为切点.令
 得,
得,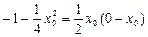 ,
,解得
 或
或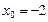 , ………
, ……… …10分
…10分故不妨取
 ,即直线
,即直线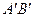 过点
过点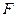 .
.综上所述,椭圆
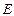 上存在一点
上存在一点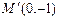 ,经过点
,经过点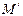 作抛物线
作抛物线 的两条切线
的两条切线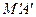 、
、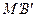 (
(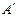 、
、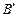 为切点),能使直线
为切点),能使直线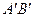 过点
过点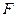 .
.此时,两切线的方程分别为
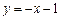 和
和 . …………11分
. …………11分抛物线
 与切线
与切线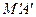 、
、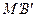 所围成图形的面积为
所围成图形的面积为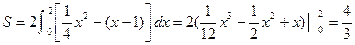 . …………13分
. …………13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
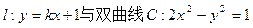 的右支交于不同的两点A、B.
的右支交于不同的两点A、B. C的右焦点F?若存在,求出k的值;若不存在,说明理由
C的右焦点F?若存在,求出k的值;若不存在,说明理由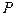 是抛物线
是抛物线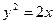 上的动点,点
上的动点,点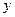 轴上的射影是
轴上的射影是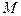 ,点
,点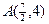 ,则
,则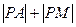 的最小值是( )
的最小值是( )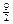
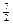
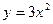 的焦点坐标是_
的焦点坐标是_ ___________________.
___________________.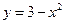 在x轴上方的曲线上,则这种矩形中面积最大值为 .
在x轴上方的曲线上,则这种矩形中面积最大值为 .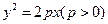 ,过定点
,过定点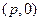 作两条互相垂直的直线
作两条互相垂直的直线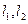 ,若
,若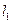 与抛物线交于点
与抛物线交于点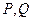 ,
,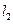 与抛物线交于
与抛物线交于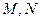 点,
点,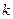 .某同学已正确求得弦
.某同学已正确求得弦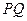 的中点坐标为
的中点坐标为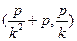 ,请写出弦
,请写出弦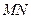 的中点坐标 .
的中点坐标 .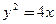 上
上 一点P到直线
一点P到直线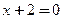 的距离是5,则点P到抛物线焦点F的距离为
的距离是5,则点P到抛物线焦点F的距离为 
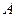 和
和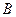 是抛物线
是抛物线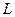 上的两个动点,且在
上的两个动点,且在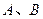 及抛物线
及抛物线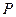 的顶点所成的三角形重心的轨迹也是一抛物线,记为
的顶点所成的三角形重心的轨迹也是一抛物线,记为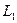 .对
.对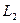 ,余类推.设如此得到抛物线的序列为
,余类推.设如此得到抛物线的序列为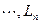 ,若抛物线
,若抛物线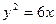 ,经专家计算得,
,经专家计算得,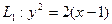 ,
, 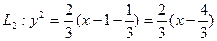 ,
,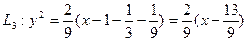 ,
, 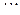 ,
, 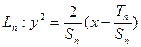 .
.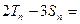 .:Z_x
.:Z_x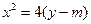 与圆
与圆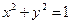 相交于第一象限的P点,且在P点处两曲线的切线互相垂直,则
相交于第一象限的P点,且在P点处两曲线的切线互相垂直,则 .
.