某校高三(1)班共有名学生.他们每天自主学习的时间全部在分钟到分钟之间.按他们学习时间的长短分个组统计,得到如下频率分布表:组别分组频数频率第一组第二组第三组第四组第五组 (1)求分布表中.的值,(2)王老师为完成一项研究.按学习时间用分层抽样的方法从这名学生中抽取名进行研究.问应抽取多少名第一组的学生?(3)已知第一组学生中男.女生人题目和参考答案——青夏教育精英家教网—

题目内容

某校高三（1）班共有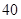名学生，他们每天自主学习的时间全部在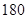分钟到分钟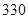之间，按他们学习时间的长短分个组统计,得到如下频率分布表：

组别	分组	频数	频率
第一组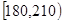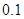
第二组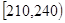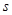
第三组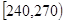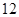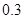
第四组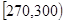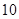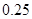
第五组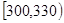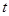

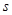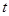（1）求分布表中

，

的值；
（2）王老师为完成一项研究，按学习时间用分层抽样的方法从这

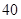名学生中抽取

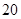名进行研究，问应抽取多少名第一组的学生？
（3）已知第一组学生中男、女生人数相同，在（2）的条件下抽取的第一组学生中，既有男生又有女生的概率是多少？

(1)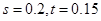(2)(3)

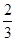
解析试题分析：
(1)第二组的频数已知,则根据根据频率的计算公式(频率=频数除以总数)即可得到频率s,再利用各组频率之和为1,即可计算得到第五组的频率t.
(2)根据抽样的原理,即在抽样过程中,保持每个个体被抽到的可能性相同,则要在40人中抽去20人,即抽取的比列为0.5,在第一组学生中抽取的比列也为0.5,即需要2人.
(3)由(2)可以知道为4选2,首先对4个人进行编号,然后列出4抽2的所有的基本事件,并计算得到满足抽取的两个人一个为女生,一个为男生的基本事件数,根据古典概型的概率计算公式即可得到相应的概率.
试题解析：
（1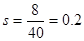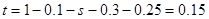），．    4分
（2）设应抽取名第一组的学生，则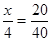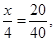得．
故应抽取2名第一组的学生．    6分
（3）在（2）的条件下应抽取2名第一组的学生，记第一组中2名男生为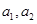，2名女生为．
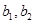按时间用分层抽样的方法抽取2名第一组的学生共有种结果，列举如下：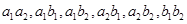
．     9分
其中既有男生又有女生被抽中的有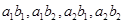这4种结果， 10分
所以既有男生又有女生被抽中的概率为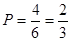.    12分
考点：古典概型频率频数分层抽样

练习册系列答案

相关题目

如图是某市3月1日至14日的空气质量指数趋势图．空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染．某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天．
(1)求此人到达当日空气质量优良的概率；
(2)求此人在该市停留期间只有1天空气重度污染的概率；
(3)由图判断从哪天开始连续三天的空气质量指数方差最大？(结论不要求证明)

爸爸和亮亮用4张扑克牌(方块2，黑桃4，黑桃5，梅花5)玩游戏，他俩将扑克牌洗匀后，背面朝上放置在桌面上，爸爸先抽，亮亮后抽，抽出的牌不放回．

(1)若爸爸恰好抽到了黑桃4．
①请把右面这种情况的树形图绘制完整；
②求亮亮抽出的牌的牌面数字比4大的概率．
(11)爸爸、亮亮约定，若爸爸抽到的牌的牌面数字比亮亮的大，则爸爸胜；反之，则亮亮赢，你认为这个游戏是否公平?如果公平，请说明理由，如果不公平，更换一张扑克牌使游戏公平．

在一次面试中，每位考生从4道题a、b、c、d中任抽两题做，假设每位考生抽到各题的可能性相等，且考生相互之间没有影响．
(1)若甲考生抽到a、b题，求乙考生与甲考生恰好有一题相同的概率；
(2)设某两位考生抽到的题中恰好有X道相同，求随机变量X的概率分布．

一个袋中装有形状大小完全相同的球9个，其中红球3个，白球6个，每次随机取1个，直到取出3次红球即停止．
(1)从袋中不放回地取球，求恰好取4次停止的概率P₁；
(2)从袋中有放回地取球．
①求恰好取5次停止的概率P₂；
②记5次之内(含5次)取到红球的个数为，求随机变量的分布列及数学期望．

某饮料公司招聘了一名员工，现对其进行一项测试，以便确定工资级别．公司准备了两种不同的饮料共8杯，其颜色完全相同，并且其中4杯为A饮料，另外4杯为B饮料，公司要求此员工一一品尝后，从8杯饮料中选出4杯A饮料，若4杯都选对，则月工资定为3500元；若4杯选对3杯，则月工资定为2 800元，否则月工资定为2100元，令X表示此人选对A饮料的杯数，假设此人对A和B两种饮料没有鉴别能力．
(1)求X的分布列：
(2)求此员工月工资的期望．

为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月（30天）的快递件数记录结果中随机抽取10天的数据，制表如下：

甲公司某员工A									乙公司某员工B
3	9	6	5	8	3	3	2	3	4	6	6	6	7	7
						0	1	4	4	2	2	2

每名快递员完成一件货物投递可获得的劳务费情况如下：
甲公司规定每件4.5元；乙公司规定每天35件以内（含35件）的部分每件4元，超出35件的部分每件7元.
（1）根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数；
（2）为了解乙公司员工B的每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为

（单位：元），求

的分布列和数学期望；
（3）根据表中数据估算两公司的每位员工在该月所得的劳务费.

某种动物由出生算起活到20岁的概率为0.8，活到25岁的概率为0.4，现有一个20岁的动物，求它能活到25岁的概率．

某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为，中奖可以获得2分；方案乙的中奖率为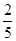，中奖可以得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品．若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≤3的概率．

试题分类