题目内容

18．若关于x的方程x3-x2-x+a=0（a∈R）有三个实根x1，x2，x3，且满足x1＜x2＜x3，则a的取值范围为（　　）
A．a＞$\frac{5}{27}$B．-$\frac{5}{27}$＜a＜1C．a＜-1D．a＞-1

分析 由x3-x2-x+a=0得-a=x3-x2-x，构造函数f（x）=x3-x2-x，利用导数求出函数f（x）的极值，即可得到结论．

解答 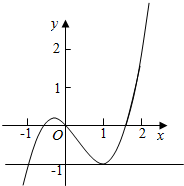解：由x3-x2-x+a=0得-a=x3-x2-x，
设f（x）=x3-x2-x，则函数的导数f′（x）=3x2-2x-1，
由f′（x）＞0得x＞1或x＜-$\frac{1}{3}$，此时函数单调递增，
由f′（x）＜0得-$\frac{1}{3}$＜x＜1，此时函数单调递减，
即函数在x=1时，取得极小值f（1）=1-1-1=-1，
在x=-$\frac{1}{3}$时，函数取得极大值f（-$\frac{1}{3}$）=（-$\frac{1}{3}$）3-（-$\frac{1}{3}$）2-（-$\frac{1}{3}$）=$\frac{5}{27}$，
要使方程x3-x2-x+a=0（a∈R）有三个实根x1，x2，x3，
则-1＜-a＜$\frac{5}{27}$，
即-$\frac{5}{27}$＜a＜1，
故选：B．

点评 本题主要考查导数的应用，构造函数，求函数的导数，利用导数求出函数的极值是解决本题的关键．

练习册系列答案
相关题目
20．（2x+1）n的展开式中的各项系数和为729，则n的值为（　　）
A．5B．6C．7D．8
9．已知函数f（x）=sin（$\frac{π}{3}$+4x）+cos（4x-$\frac{π}{6}$）
（1）求该函数的单调区间，最大、最小值；
（2）设g（x）=f（x+a），若g（x）的图象关于y轴对称，求实数a的最小正值．
6．已知函数f（x）=cos2（x+$\frac{π}{4}$），a=f（lg8），b=f（lg$\frac{1}{8}$），则（　　）
A．a+b=0B．a-b=0C．a+b=1D．a-b=1
13．数列{an}共有12项，其中a1=0，a5=-2，a12=3，且|ak+1-ak|=1（k=1，2，3，…11），则满足这种条件的不同数列的个数为28．
3．已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=-4+cosθ}\\{y=sinθ}\end{array}\right.$，θ∈[π，2π]，若以坐标原点O为极点，x轴正半轴为极轴，曲线C2的极坐标方程为$ρsin（{θ+\frac{π}{4}}）=\sqrt{2}（{ρ＞0，θ∈[{0，\frac{π}{2}}]}）$，那么C1上的点到曲线C2上的点的距离的最小值为$2\sqrt{5}$-1．
10．已知a、b为实数，则“a＞b＞1”是“$\frac{1}{a-1}$＜$\frac{1}{b-1}$”的充分不必要条件（填“充分不必要”、“必要不充分”及“充要”等）．
7．设等差数列 {an}的前n项和为Sn，若S12=288，S9=162，则S6=（　　）
A．18B．36C．54D．72
8．等边三角形ABC的两个顶点坐标分别为A（4，-6），B（-2，-6），求点C的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网