题目内容
3.已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=-4+cosθ}\\{y=sinθ}\end{array}\right.$,θ∈[π,2π],若以坐标原点O为极点,x轴正半轴为极轴,曲线C2的极坐标方程为$ρsin({θ+\frac{π}{4}})=\sqrt{2}({ρ>0,θ∈[{0,\frac{π}{2}}]})$,那么C1上的点到曲线C2上的点的距离的最小值为$2\sqrt{5}$-1.分析 曲线C1的参数方程为$\left\{\begin{array}{l}{x=-4+cosθ}\\{y=sinθ}\end{array}\right.$,θ∈[π,2π],利用cos2θ+sin2θ=1即可化为直角坐标方程.曲线C2的极坐标方程为$ρsin({θ+\frac{π}{4}})=\sqrt{2}({ρ>0,θ∈[{0,\frac{π}{2}}]})$,展开为$\frac{\sqrt{2}}{2}(ρsinθ+ρcosθ)$=$\sqrt{2}$,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得到直角坐标方程.即可得出C1上的点到曲线C2上的点的距离的最小值.
解答 解:曲线C1的参数方程为$\left\{\begin{array}{l}{x=-4+cosθ}\\{y=sinθ}\end{array}\right.$,θ∈[π,2π],化为(x+4)2+y2=1,可得圆心C1(-4,0),半径r=1.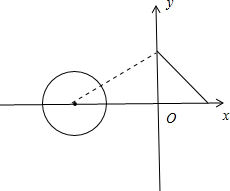
曲线C2的极坐标方程为$ρsin({θ+\frac{π}{4}})=\sqrt{2}({ρ>0,θ∈[{0,\frac{π}{2}}]})$,展开为$\frac{\sqrt{2}}{2}(ρsinθ+ρcosθ)$=$\sqrt{2}$,
∴y+x-2=0.(x,y≥0).
∴C1上的点到曲线C2上的点的距离的最小值d=$\sqrt{(-4)^{2}+{2}^{2}}$-1=2$\sqrt{5}$-1.
故答案为:$2\sqrt{5}$-1.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、两点之间的距离公式,考查了数形结合方法、推理能力与计算能力,属于中档题.


| A. | f(x)=-x2+1 | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=lg$\frac{1+x}{1-x}$ | D. | f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$ |
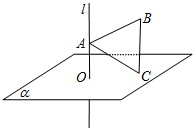 如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )| A. | $1+\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{3}$ | D. | $2+\sqrt{3}$ |
| A. | a>$\frac{5}{27}$ | B. | -$\frac{5}{27}$<a<1 | C. | a<-1 | D. | a>-1 |
| A. | -1 | B. | -2 | C. | -3 | D. | -3或-2 |
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
| A. | f(sinα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(cosα)>f(cosβ) |