题目内容
6.已知函数f(x)=cos2(x+$\frac{π}{4}$),a=f(lg8),b=f(lg$\frac{1}{8}$),则( )| A. | a+b=0 | B. | a-b=0 | C. | a+b=1 | D. | a-b=1 |
分析 由条件利用三角恒等变换化简函数f(x)的解析式,再利用诱导公式化简a+b,可得结果.
解答 解:函数f(x)=cos2(x+$\frac{π}{4}$)=$\frac{1+cos(2x+\frac{π}{2})}{2}$=-$\frac{1}{2}$sin2x+$\frac{1}{2}$,
又a=f(lg8),b=f(lg$\frac{1}{8}$),
∴a+b=-$\frac{1}{2}$sin(lg8)+$\frac{1}{2}$-$\frac{1}{2}$sin(-lg8)+$\frac{1}{2}$=1,
故选:C.
点评 本题主要考查三角恒等变换、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
8.已知集合A={-1,i},i为虚数单位,则下列选项正确的是( )
| A. | $\frac{1}{i}$∈A | B. | $\frac{1-i}{1+i}$∈A | C. | i3∈A | D. | |-i|∈A |
9.两条平行的直线分别经过点A(3,0),B(0,4),它们之间的距离d满足的条件是( )
| A. | 0<d≤3 | B. | 0<d≤5 | C. | 0<d≤4 | D. | 3<d≤5 |
14.某流程图如图所示,现输入如下四个函数,则可以输出f(x)的是( )
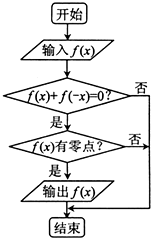

| A. | f(x)=-x2+1 | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=lg$\frac{1+x}{1-x}$ | D. | f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$ |
1.已知过x轴上一点E(x0,0)(0<x0<$\sqrt{2}$)的直线l与椭圆$\frac{{x}^{2}}{2}$+y2=1相交于M、N两点,若$\frac{1}{E{M}^{2}}$+$\frac{1}{E{N}^{2}}$为定值,则x0的值为( )
| A. | 1 | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
11. 如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
 如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )| A. | $1+\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{3}$ | D. | $2+\sqrt{3}$ |
18.若关于x的方程x3-x2-x+a=0(a∈R)有三个实根x1,x2,x3,且满足x1<x2<x3,则a的取值范围为( )
| A. | a>$\frac{5}{27}$ | B. | -$\frac{5}{27}$<a<1 | C. | a<-1 | D. | a>-1 |
15.已知过点A(1,m)恰能作曲线f(x)=x3-3x的两条切线,则m的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | -3或-2 |