题目内容
9.已知函数f(x)=sin($\frac{π}{3}$+4x)+cos(4x-$\frac{π}{6}$)(1)求该函数的单调区间,最大、最小值;
(2)设g(x)=f(x+a),若g(x)的图象关于y轴对称,求实数a的最小正值.
分析 (1)利用诱导公式对原函数解析式化简,进而利用三角函数图象与性质求得函数的最大最小值,以及单调区间.
(2)先确定g(x)的解析式,进而利用三角函数的性质求得a的最小值.
解答 解(1)f(x)=sin($\frac{π}{3}$+4x)+cos(4x-$\frac{π}{6}$)=sin($\frac{π}{3}$+4x)+sin($\frac{π}{3}$+4x)=2sin(4x+$\frac{π}{3}$),
∴函数f(x)的最大值为2,最小值为-2,
由2kπ+$\frac{π}{2}$≤4x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈Z,求得递减区间[$\frac{π}{24}$+$\frac{kπ}{2}$,$\frac{7π}{24}$+$\frac{kπ}{2}$](k∈Z),
由2kπ-$\frac{π}{2}$≤4x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,求得递增区间[-$\frac{5π}{24}$+$\frac{kπ}{2}$,$\frac{π}{24}$+$\frac{kπ}{2}$](k∈Z).
(2)g(x)=2sin[4(x+a)+$\frac{π}{3}$],
图象关于y轴对称,得到g(x)=2cos4x,
则4a+$\frac{π}{3}$=$\frac{π}{2}$+2kπ,
∴a=$\frac{kπ}{2}$+$\frac{π}{24}$,k∈Z.
∴a最小正值$\frac{π}{24}$.
点评 本题主要考查了三角函数图象与性质,诱导公式的应用.注意在解题过程中与函数的图象相结合.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
11.已知函数f(x)是奇函数(x∈R),则( )
| A. | f(x)•sinx是奇函数 | B. | f(x)+cosx是偶函数 | ||
| C. | f(x2)•sinx是奇函数 | D. | f(x2)+sinx是偶函数 |
9.两条平行的直线分别经过点A(3,0),B(0,4),它们之间的距离d满足的条件是( )
| A. | 0<d≤3 | B. | 0<d≤5 | C. | 0<d≤4 | D. | 3<d≤5 |
14.某流程图如图所示,现输入如下四个函数,则可以输出f(x)的是( )
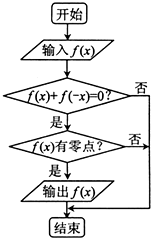

| A. | f(x)=-x2+1 | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=lg$\frac{1+x}{1-x}$ | D. | f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$ |
1.已知过x轴上一点E(x0,0)(0<x0<$\sqrt{2}$)的直线l与椭圆$\frac{{x}^{2}}{2}$+y2=1相交于M、N两点,若$\frac{1}{E{M}^{2}}$+$\frac{1}{E{N}^{2}}$为定值,则x0的值为( )
| A. | 1 | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
18.若关于x的方程x3-x2-x+a=0(a∈R)有三个实根x1,x2,x3,且满足x1<x2<x3,则a的取值范围为( )
| A. | a>$\frac{5}{27}$ | B. | -$\frac{5}{27}$<a<1 | C. | a<-1 | D. | a>-1 |