题目内容
【题目】已知奇函数f(x)定义域为(﹣∞,0)∪(0,+∞),f′(x)为其导函数,且满足以下条件①x>0时,f′(x)< ![]() ;②f(1)=
;②f(1)= ![]() ;③f(2x)=2f(x),则不等式
;③f(2x)=2f(x),则不等式 ![]() <2x2的解集为 .
<2x2的解集为 .
【答案】(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
【解析】解:令F(x)= ![]() ,则F′(x)=
,则F′(x)= ![]() ,
,
∵x>0时,f′(x)< ![]() ,
,
∴F′(x)<0,
∴F(x)在(0,+∞)上单调递减,又f(x)为奇函数,
∴F(x)= ![]() 为偶函数,
为偶函数,
∴F(x)在(﹣∞,0)上单调递增,
又f(1)= ![]() ,f(2x)=2f(x),
,f(2x)=2f(x),
∴f( ![]() )=
)= ![]() f(1)=
f(1)= ![]() ,f(
,f( ![]() )=
)= ![]() f(
f( ![]() )=
)= ![]() ,
,
∴F( ![]() )=
)= ![]() =8,
=8,
∴ ![]() <2x2等价于
<2x2等价于 ![]() <8,即F(x)<F(
<8,即F(x)<F( ![]() ),故|x|>
),故|x|> ![]() ,
,
解得:x> ![]() 或x<﹣
或x<﹣ ![]() .
.
所以答案是:(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞).
,+∞).
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

【题目】某校为调查高中生选修课的选修倾向与性别关系,随机抽取50名学生,得到如表的数据表:
倾向“平面几何选讲” | 倾向“坐标系与参数方程” | 倾向“不等式选讲” | 合计 | |
男生 | 16 | 4 | 6 | 26 |
女生 | 4 | 8 | 12 | 24 |
合计 | 20 | 12 | 18 | 50 |
(1)根据表中提供的数据,选择可直观判断“选课倾向与性别有关系”的两种,作为选课倾向的变量的取值,并分析哪两种选择倾向与性别有关系的把握大;
附:K2= ![]() .
.
P(k2≤k0) | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(2)在抽取的50名学生中,按照分层抽样的方法,从倾向“平面几何选讲”与倾向“坐标系与参数方程”的学生中抽取8人进行问卷.若从这8人中任选3人,记倾向“平面几何选讲”的人数减去与倾向“坐标系与参数方程”的人数的差为ξ,求ξ的分布列及数学期望.
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
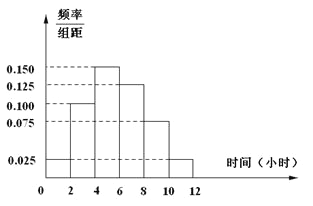
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
