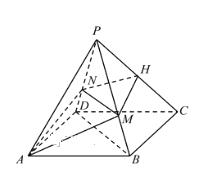
[题目]如图,在棱长均相等的四棱锥中, 为底面正方形的中心, ,分别为侧棱,的中点,有下列结论正确的有:( )A.∥平面B.平面∥平面C.直线与直线所成角的大小为D. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图,在棱长均相等的四棱锥中, 为底面正方形的中心, ,分别为侧棱,的中点,有下列结论正确的有：( )

A.∥平面B.平面∥平面

C.直线与直线所成角的大小为D.

【答案】ABD

【解析】

选项A,利用线面平行的判定定理即可证明；选项B,先利用线面平行的判定定理证明CD∥平面OMN，再利用面面平行的判定定理即可证明；选项C，平移直线，找到线面角，再计算；选项D,因为ON∥PD，所以只需证明PD⊥PB，利用勾股定理证明即可.

选项A,连接BD，显然O为BD的中点，又N为PB的中点，所以∥ON,由线面平行的判定定理可得，∥平面；选项B, 由,分别为侧棱,的中点,得MN∥AB,又底面为正方形，所以MN∥CD，由线面平行的判定定理可得，CD∥平面OMN,又选项A得∥平面，由面面平行的判定定理可得，平面∥平面；选项C,因为MN∥CD，所以∠ PDC为直线与直线所成的角，又因为所有棱长都相等，所以∠ PDC=，故直线与直线所成角的大小为；选项D，因底面为正方形，所以,又所有棱长都相等，所以,故,又

∥ON，所以，故ABD均正确.

练习册系列答案

投资A商品金额（万元）	1	2	3	4	5	6
获纯利润（万元）	0.65	1.39	1.85	2	1.84	1.40
投资B商品金额（万元）	1	2	3	4	5	6
获纯利润（万元）	0.25	0.49	0.76	1	1.26	1.51

该经营者准备下月投入12万元经营这两种产品，但不知投入A、B两种商品各多少才最合算．请你帮助制定一下资金投入方案，使得该经营者能获得最大利润，并按你的方案求出该经营者下月可获得的最大利润（结果保留两个有效数字）．

【题目】在古代，直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”，斜边称为“弦”.三国时期吴国数学家赵爽用“弦图”( 如图) 证明了勾股定理，证明方法叙述为:“按弦图,又可以勾股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实，亦成弦实.”这里的“实”可以理解为面积.这个证明过程体现的是这样一个等量关系:“两条直角边的乘积是两个全等直角三角形的面积的和(朱实二 )，4个全等的直角三角形的面积的和(朱实四) 加上中间小正方形的面积(黄实) 等于大正方形的面积(弦实)”. 若弦图中“弦实”为16，“朱实一”为,现随机向弦图内投入一粒黄豆(大小忽略不计)，则其落入小正方形内的概率为( )