题目内容
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() 于点
于点![]() ,且
,且![]() 平面
平面![]() .
.
(1)证明: ![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面AMHN与平面ABCD所成锐二面角的余弦值.
,求平面AMHN与平面ABCD所成锐二面角的余弦值.
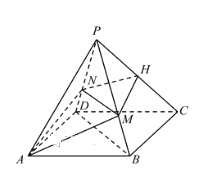
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:
(1)连![]() 交
交![]() 于点
于点![]() ,连
,连![]() ,则得
,则得![]() ,进而可得
,进而可得![]() 平面
平面![]() ,于是
,于是![]() .由线面平行的性质可得
.由线面平行的性质可得![]() ,所以得
,所以得![]() .(2)由条件可得
.(2)由条件可得![]() 两两垂直,建立空间直角坐标系,然后分别求出平面AMHN与平面ABCD的法向量,通过两法向量的夹角的余弦值可得所求.
两两垂直,建立空间直角坐标系,然后分别求出平面AMHN与平面ABCD的法向量,通过两法向量的夹角的余弦值可得所求.
试题解析:
(1)证明:连![]() 交
交![]() 于点
于点![]() ,连
,连![]() .
.
因为四边形![]() 为菱形,
为菱形,
所以![]() ,且
,且![]() 为
为![]() 、
、![]() 的中点.
的中点.
因为![]() ,
,
所以![]() ,
,
又![]() 且
且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,
,
所以![]() .
.
(2)由(1)知![]() 且
且![]() ,
,
因为![]() ,且
,且![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() .
.
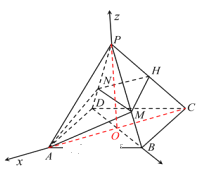
分别以![]() 为
为![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系![]() .
.
设![]() ,则
,则![]()
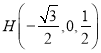 ,
,
所以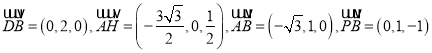
设平面![]() 的法向量为
的法向量为![]() ,
,
则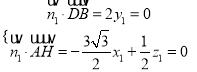 ,令
,令![]() ,得
,得![]() .
.
由题意可得平面![]() 的法向量为
的法向量为![]() ,
,
所以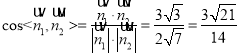 .
.
所以平面AMHN与平面ABCD所成锐二面角的余弦值为![]() .
.

【题目】如图所示,图①是棱长为1的小正方体,图②,③是由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别将第1层,第2层,…,第![]() 层的小正方体的个数记为
层的小正方体的个数记为![]() ,解答下列问题:
,解答下列问题:
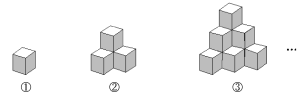
(1)按照要求填表:
| 1 | 2 | 3 | 4 | … |
| 1 | 3 | 6 | _ | … |
(2)![]() __________.
__________.
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数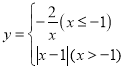 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
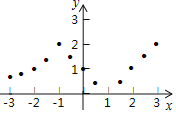
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
