题目内容
16.若a,b,c∈R+,求证:2[($\frac{a+b}{2}$-$\sqrt{ab}$]≤3[$\frac{a+b+c}{3}$-$\root{3}{abc}$].分析 把原不等式进行等价转化,原不等式等价于证明 $\frac{c+\sqrt{ab}+\sqrt{ab}}{3}$≥$\root{3}{abc}$,由基本不等式证明即可.
解答 证明:不等式2[($\frac{a+b}{2}$-$\sqrt{ab}$]≤3[$\frac{a+b+c}{3}$-$\root{3}{abc}$]等价于
a+b-2$\sqrt{ab}$≤a+b+c-3$\root{3}{abc}$,
等价于3$\root{3}{abc}$≤c+$\sqrt{ab}$+$\sqrt{ab}$,
等价于c+$\sqrt{ab}$+$\sqrt{ab}$≥3$\root{3}{abc}$①
等价于$\frac{c+\sqrt{ab}+\sqrt{ab}}{3}$≥$\root{3}{abc}$,
∵x,y,z∈R+,
由基本不等式 $\frac{x+y+z}{3}$≥$\root{3}{xyz}$知,①成立.
∴原不等式成立.
点评 本题考查不等式的证明,主要考查基本不等式的应用,体现转化的数学思想方法.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
7.已知正数等比数列{an},a1=1,a3=2,则a1a2+a3a4+a5a6+…+a2n-1a2n的值为( )
| A. | $\sqrt{2}$(2n-1) | B. | 2(2n-1) | C. | $\frac{\sqrt{2}({4}^{n}-1)}{3}$ | D. | $\frac{2({4}^{n}-1)}{3}$ |
11.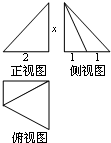 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )| A. | 9 | B. | 8 | C. | 3 | D. | 6 |
5.已知${∫}_{0}^{t}$xdx=2,则${∫}_{-t}^{0}$xdx等于( )
| A. | 0 | B. | 2 | C. | -1 | D. | -2 |

 已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45°
已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45° 在极坐标系中,已知圆C的圆心在点C(2,0)且经过极点O,点P(6,0).
在极坐标系中,已知圆C的圆心在点C(2,0)且经过极点O,点P(6,0).