Question

【题目】如图，三棱柱ABC﹣A1B1C1中，∠ACB=90°，CC1⊥底面ABC，AC=BC=CC1=2，D，E，F分别是棱AB，BC，B1C1的中点，G是棱BB1上的动点．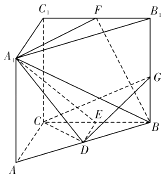
（1）当 为何值时，平面CDG⊥平面A1DE？
（2）求平面AB1F与平面AD1E所成的锐二面角的余弦值．

Answer 1

【答案】
（1）解：当G为BB1中点（即 ）时，平面CDG⊥平面A1DE．

证明如下：由于DE∥AC且 ，∴ ，故D，E，C1，A1四点共面．

连接C1E交GC于H．在正方形CBB1C1中， ，故∠CHE=90°，即CG⊥C1E．又A1C1⊥平面CBB1C1，CG平面CBB1C1，所以DE⊥CG，又因为C1E∩DE=E，故CG⊥平面A1DE，从而平面CDG⊥平面A1DE

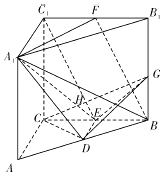
（2）解：三棱柱ABC﹣A1B1C1中，∠ACB=90°，CC1⊥底面ABC，

于是可以以C为原点，CA，CB，CC1所在的直线分别为x，y，z轴建立空间直角坐标系，

如图所示．

因为AC=BC=CC1=2，D，E，F分别是棱AB，BC，B1C1的中点，

所以A1（2，0，2），D（1，1，0），E（0，1，0），B（0，2，0），F（0，1，2），

G（0，2.1）， =（﹣2，2，﹣2）， =（﹣2，1，0）．

由（1）知平面A1DE的法向量为 =（0，2，1），

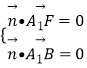设平面A1BF的法向量为 =（x，y，z），则 ，即： ，

令x=1得 ，

设平面A1BF与平面A1DE所成的锐二面角为θ，

则cosθ= = = ．

【解析】（1）当G为BB1中点（即 ）时，平面CDG⊥平面A1DE．证明D，E，C1 ， A1四点共面．连接C1E交GC于H．证明CG⊥C1E．DE⊥CG，推出CG⊥平面A1DE，即可证明平面CDG⊥平面A1DE．（2）以C为原点，CA，CB，CC1所在的直线分别为x，y，z轴建立空间直角坐标系，求出平面A1DE的法向量，平面A1BF的法向量，设平面A1BF与平面A1DE所成的锐二面角为θ，利用数量积求解即可．
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．