题目内容
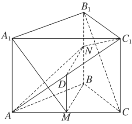
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.![]() ,
,![]() ,
,![]() .
.
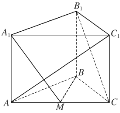
(1)求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)见解析(2)存在,![]()
【解析】
(1)易证![]() ,又可证
,又可证![]() ,由
,由![]() ,
,![]() ,
,![]() ,可求
,可求![]() ,从而可证
,从而可证![]() ,从而证明
,从而证明![]() 平面
平面![]() .
.
(2)当点![]() 为
为![]() 的中点,可证平面
的中点,可证平面![]() 平面
平面![]() ,设
,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() ,可证
,可证![]() ,由
,由![]() 平面
平面![]() ,可证
,可证![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() .
.
(1)证明:∵侧棱![]() 底面
底面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() 为棱
为棱![]() 的中点,
的中点, ![]() ,∴
,∴![]() .
.
∵![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() .又∵
.又∵![]() ,∴在
,∴在![]() 和
和![]() 中,
中, ![]() ,
,
∴![]() ,
,
即![]() ,∴
,∴![]()
∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:当点![]() 为
为![]() 的中点,即
的中点,即![]() 时,平面
时,平面![]() 平面
平面![]()
证明如下:
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() ,∵
,∵![]() ,
,![]() 分别为
分别为![]() ,
, ![]() 的中点,∴
的中点,∴![]() ,
,
且![]() .又∵
.又∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .又∵
.又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.

练习册系列答案
相关题目
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程.
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式用最小二乘法求线性回归方程系数公式: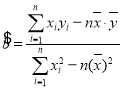 ,
,![]() .
.