Question

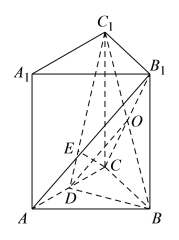
【题目】如图，在三棱柱中，各个侧面均是边长为的正方形，为线段的中点

（Ⅰ）求证：⊥平面；

（Ⅱ）求证：直线∥平面；

（Ⅲ）设为线段上任意一点，在内的平面区域（包括边界）是否存在点，使，并说明理由

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析

【解析】

（1）充分利用正三棱柱的性质得到CC1⊥底面ABC，得到CC1⊥BD，只要再证明BD垂直于AC即可；

（2）连接B1C交BC1于O，连接OD，D为AC 中点，得到AB1∥OD，利用线面平行的判定定理可得；

（3）在△BC1D内的平面区域（包括边界）存在点E，使CE⊥DM，此时E在线段C1D上；只要利用线面垂直的判定定理和性质定理证明．

（）证明：∵三棱柱中，各个侧面均是边长为的正方形，

∴，，

∴平面，

又∵平面，

∴，

又底面为等边三角形，为线段的中点，

∴，

又，

∴平面．

（）证明：连接交于，连接，则为的中点，

∵是的中点，

∴，

又平面，平面，

∴直线平面．

（）在内的平面区域（包括边界）存在点，使，此时在线段上，

证明如下：过作交线段与，

由（）可知，平面，而平面，

∴，

由，，得平面，

∵平面，

∴．