题目内容
7．已知0＜a＜2，l1：ax-2y=2a-4，l2：2x+a2y=2a2+4，求l1，l2与坐标轴围成的四边形面积的最小值．分析 如图所示，联立$\left\{\begin{array}{l}{ax-2y=2a-4}\\{2x+{a}^{2}y=2{a}^{2}+4}\end{array}\right.$，解得yE=2．根据S四边形OCEA=S△BCE-S△OAB即可得出．
解答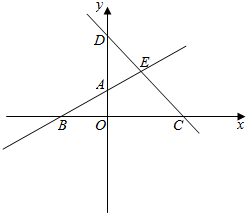 
解：∵0＜a＜2，
可得l1：ax-2y=2a-4，与坐标轴的交点A（0，-a+2），B（2-$\frac{4}{a}$，0）．
l2：2x+a2y=2a2+4，与坐标轴的交点C（a2+2，0），D$（0，2+\frac{4}{{a}^{2}}）$．
联立$\left\{\begin{array}{l}{ax-2y=2a-4}\\{2x+{a}^{2}y=2{a}^{2}+4}\end{array}\right.$，解得yE=2．
∴S四边形OCEA=S△BCE-S△OAB
=$\frac{1}{2}|BC|•{y}_{E}$-$\frac{1}{2}|OA|•|OB|$
=${a}^{2}+\frac{4}{a}$-$\frac{1}{2}×（2-a）×（\frac{4}{a}-2）$
=a2-a+4
=$（a-\frac{1}{2}）^{2}$+$\frac{15}{4}$$≥\frac{15}{4}$，当a=$\frac{1}{2}$时取等号．
∴l1，l2与坐标轴围成的四边形面积的最小值为$\frac{15}{4}$．
点评 本题考查了相交直线、三角形的面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
19．已知函数f（x）=|ex-1|+1，若f（a）=f（b），且a＜b，则实数a+2b的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，ln$\frac{4}{3}$） | C． | （-∞，ln3] | D． | （-∞，ln$\frac{32}{37}$] |