题目内容
17.O为△ABC的重心,若OA=1,OB=$\frac{\sqrt{6}+\sqrt{2}}{2}$,∠AOB=$\frac{π}{4}$,则OC=$\sqrt{4+2\sqrt{6}}$.分析 由题意画出图形,利用余弦定理求得重心O到AB中点的距离,然后结合重心的性质求得OC.
解答 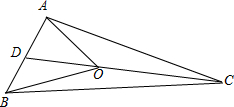 解:如图,
解:如图,
在△AOB中,OA=1,OB=$\frac{\sqrt{6}+\sqrt{2}}{2}$,∠AOB=$\frac{π}{4}$,
由余弦定理可得,$AB=\sqrt{O{A}^{2}+O{B}^{2}-2OA•OB•cos∠AOB}$
=$\sqrt{{1}^{2}+(\frac{\sqrt{6}+\sqrt{2}}{2})^{2}-2×1×\frac{\sqrt{6}+\sqrt{2}}{2}×\frac{\sqrt{2}}{2}}$=$\sqrt{2}$.
∴AD=DB=$\frac{\sqrt{2}}{2}$.
设OD=x,
则$cos∠ADO=\frac{O{D}^{2}+A{D}^{2}-O{A}^{2}}{2•OD•DA}$=$\frac{{x}^{2}+(\frac{\sqrt{2}}{2})^{2}-{1}^{2}}{\sqrt{2}x}$,
$cos∠BDO=\frac{O{D}^{2}+B{D}^{2}-O{B}^{2}}{2•OD•BD}$=$\frac{{x}^{2}+(\frac{\sqrt{2}}{2})^{2}-(\frac{\sqrt{6}+\sqrt{2}}{2})^{2}}{\sqrt{2}x}$.
∴$2{x}^{2}+2×(\frac{\sqrt{2}}{2})^{2}-1-(\frac{\sqrt{6}+\sqrt{2}}{2})^{2}=0$,解得:$x=\sqrt{1+\sqrt{\frac{3}{2}}}$.
∴OC=2x=$\sqrt{4+2\sqrt{6}}$.
故答案为:$\sqrt{4+2\sqrt{6}}$.
点评 本题考查三角形的解法,考查了余弦定理的应用,考查计算能力,是中档题.

 小学教材完全解读系列答案
小学教材完全解读系列答案