题目内容
设集合A={(x,y)|(x-4)2+y2=1},B={(x,y)|(x-t)2+(y-at+2)2=1}.如果命题“?t∈R,A∩B≠ ”是真命题,则实数a的取值范围是 .
”是真命题,则实数a的取值范围是 .
 ”是真命题,则实数a的取值范围是 .
”是真命题,则实数a的取值范围是 . 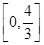
集合A、B分别表示两个圆,
圆心M(4,0),r1=1,
N(t,at-2),r2=1,
?t∈R,A∩B≠ ,则两圆一定有公共点,
,则两圆一定有公共点,
|MN|=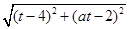 ,0≤|MN|≤2,
,0≤|MN|≤2,
即|MN|2≤4,化简得,
(a2+1)t2-(8+4a)t+16≤0.
∵a2+1>0,
∴Δ=(8+4a)2-4(a2+1)×16≥0,
即3a2-4a≤0,
∴0≤a≤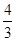 .
.
圆心M(4,0),r1=1,
N(t,at-2),r2=1,
?t∈R,A∩B≠
 ,则两圆一定有公共点,
,则两圆一定有公共点,|MN|=
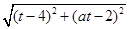 ,0≤|MN|≤2,
,0≤|MN|≤2,即|MN|2≤4,化简得,
(a2+1)t2-(8+4a)t+16≤0.
∵a2+1>0,
∴Δ=(8+4a)2-4(a2+1)×16≥0,
即3a2-4a≤0,
∴0≤a≤
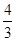 .
.
练习册系列答案
相关题目
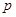 :方程
:方程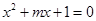 有两个不等的负实根,命题
有两个不等的负实根,命题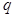 :方程
:方程 无实根。若
无实根。若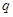 为真,
为真,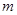 的取值范围.
的取值范围.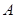 .函数
.函数 为
为 上可导函数,则
上可导函数,则 是
是 为函数
为函数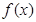 极值点的充要条件.
极值点的充要条件. .命题“
.命题“ ”的否定是“
”的否定是“ ”.
”. .命题“在
.命题“在 中,若
中,若 ”的逆命题为假命题.
”的逆命题为假命题. .“
.“ ”是“函数
”是“函数 是偶函数”的充要条件.
是偶函数”的充要条件.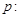
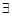
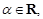
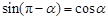 命题
命题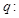
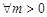 ,双曲线
,双曲线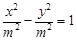 的离心率为
的离心率为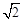 ,则下面结论正确的是( )
,则下面结论正确的是( )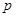 是假命题
是假命题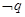 是真命题
是真命题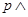
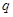 是假命题
是假命题 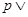
 ,则
,则 ”的否命题为:“若
”的否命题为:“若 ”
” ,则命题
,则命题
 ,则
,则 ”的逆否命题为真命题
”的逆否命题为真命题 ”是“
”是“ ”的必要不充分条件
”的必要不充分条件 -
- =1为双曲线,命题q:函数f(x)=(4-a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是________.
=1为双曲线,命题q:函数f(x)=(4-a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是________.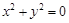 ,则
,则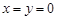 ”,在它的逆命题、否命题、逆否命题中,真命题的个数是
”,在它的逆命题、否命题、逆否命题中,真命题的个数是