题目内容
椭圆E的中心在原点O,焦点在x轴上,离心率e=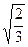 ,过点C(-1,0)的直线
,过点C(-1,0)的直线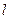 交椭圆于A,B两点,且满足
交椭圆于A,B两点,且满足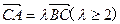 ,
,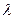 为常数。
为常数。
(1)当直线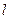 的斜率k=1且
的斜率k=1且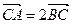 时,求三角形OAB的面积.
时,求三角形OAB的面积.
(2)当三角形OAB的面积取得最大值时,求椭圆E的方程.
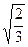 ,过点C(-1,0)的直线
,过点C(-1,0)的直线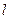 交椭圆于A,B两点,且满足
交椭圆于A,B两点,且满足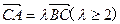 ,
,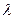 为常数。
为常数。(1)当直线
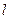 的斜率k=1且
的斜率k=1且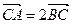 时,求三角形OAB的面积.
时,求三角形OAB的面积. (2)当三角形OAB的面积取得最大值时,求椭圆E的方程.
(1)
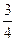
(2)

(1)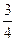
(2)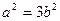 ,故椭圆为:
,故椭圆为: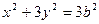 ①
①
且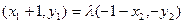 ②,把
②,把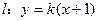 代入椭圆方程得:
代入椭圆方程得:

∴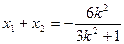 ③
③ 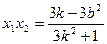 ④
④
∴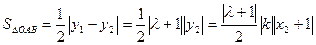
由②③知道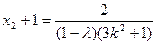
∴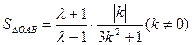
⑵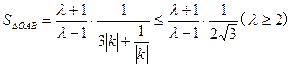
当且仅当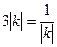 时,即
时,即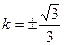 时,S取得最大值。
时,S取得最大值。
将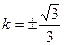 代入③④得
代入③④得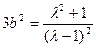 ,
,
∴
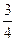
(2)
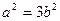 ,故椭圆为:
,故椭圆为: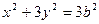 ①
①且
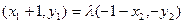 ②,把
②,把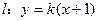 代入椭圆方程得:
代入椭圆方程得:
∴
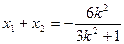 ③
③ 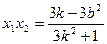 ④
④∴
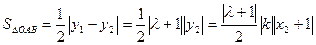
由②③知道
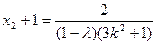
∴
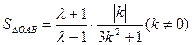
⑵
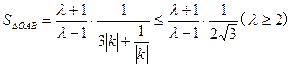
当且仅当
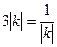 时,即
时,即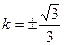 时,S取得最大值。
时,S取得最大值。将
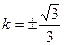 代入③④得
代入③④得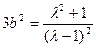 ,
,∴


练习册系列答案
相关题目
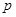 是椭圆
是椭圆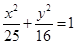 上的点.若
上的点.若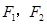 是椭圆的两个焦点,则
是椭圆的两个焦点,则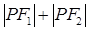 等于( )
等于( )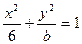 (
(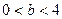 ),抛物线方程为
),抛物线方程为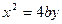 .过抛物线的焦点作
.过抛物线的焦点作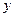 轴的垂线,与抛物线在第一象限的交点为
轴的垂线,与抛物线在第一象限的交点为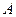 ,抛物线在点
,抛物线在点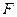 .
. 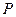 为椭圆上的动点,由
为椭圆上的动点,由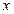 轴作垂线
轴作垂线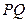 ,垂足为
,垂足为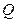 ,且直线
,且直线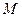 满足
满足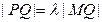 ,求点
,求点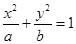 和直线
和直线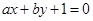 (
(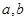 为非零实数)在同一坐标系中,它们的图形可能是( )
为非零实数)在同一坐标系中,它们的图形可能是( )
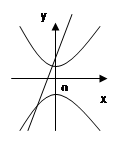

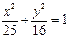 ,P为该椭圆上一点.
,P为该椭圆上一点.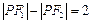 ,求
,求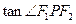 的值
的值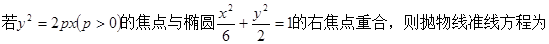 ( )
( )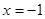
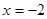
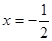
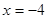
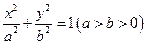 的两个焦点为
的两个焦点为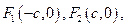
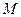 是椭圆上一点,且满
是椭圆上一点,且满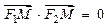 .
.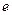 的取值
的取值 范围;
范围;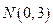 到椭圆上点的最远距离为
到椭圆上点的最远距离为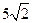 .
.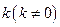 的直线
的直线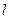 与椭圆G相交于不同两点
与椭圆G相交于不同两点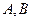 ,
,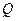 为
为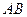 的中点,问:
的中点,问:
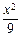 +
+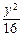 =1的两焦点为F1、F2,点P在椭圆上,且直线PF1、PF2的夹角为
=1的两焦点为F1、F2,点P在椭圆上,且直线PF1、PF2的夹角为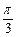 ,则△PF1F2的面积为
,则△PF1F2的面积为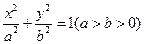 的左,右焦点为
的左,右焦点为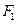 ,
,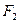 ,(1,
,(1,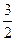 )为椭圆上一点,椭圆的
)为椭圆上一点,椭圆的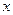 轴的对称点记为M,设
轴的对称点记为M,设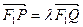 .
.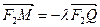 ;
;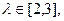 求|PQ|的取值范围
求|PQ|的取值范围