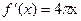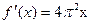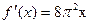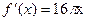题目内容
设函数 (
(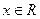 ),其中
),其中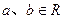 .
.
(1)当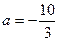 时,讨论函数
时,讨论函数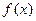 的单调性;
的单调性;
(2)若函数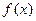 仅在
仅在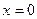 处有极值,求
处有极值,求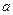 的取值范围;
的取值范围;
(3)若对于任意的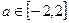 ,不等式
,不等式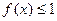 在
在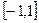 上恒成立,求
上恒成立,求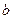 的取值范围.
的取值范围.
 (
(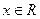 ),其中
),其中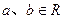 .
.(1)当
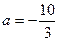 时,讨论函数
时,讨论函数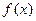 的单调性;
的单调性;(2)若函数
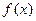 仅在
仅在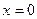 处有极值,求
处有极值,求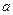 的取值范围;
的取值范围;(3)若对于任意的
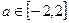 ,不等式
,不等式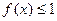 在
在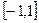 上恒成立,求
上恒成立,求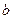 的取值范围.
的取值范围.解:(1) =
=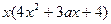 ,
,
当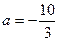 时
时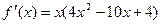 =
=
令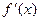 =0,解得
=0,解得 .
.
?
当x变化时,f′(x),f(x)的变化情况如下表:
所以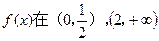 内是增函数,
内是增函数,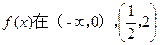 内是减函数……….4分
内是减函数……….4分

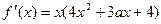 ,显然
,显然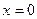 不是方程
不是方程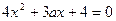 的根,为使
的根,为使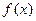
仅在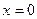 处有极值,必须有
处有极值,必须有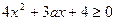 恒成立,即有
恒成立,即有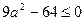 ,解得
,解得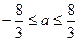 ,
,
这时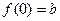 是唯一极值。因此,满足条件的a的取值范围是
是唯一极值。因此,满足条件的a的取值范围是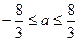 .………….8分
.………….8分
(3)由条件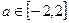 可知
可知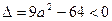 ,从而
,从而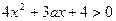 恒成立.
恒成立.
当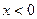 时,
时,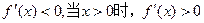 。
。
因此函数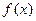 在
在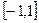 上的最大值是
上的最大值是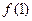 与
与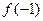 两者中的最大者。
两者中的最大者。
为使对任意的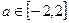 ,不等式
,不等式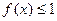 在
在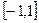 上恒成立,
上恒成立,
当且仅当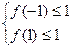 ,即
,即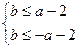 ,
,
所以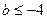 ,因此满足条件的
,因此满足条件的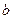 的取值范围是
的取值范围是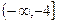 .……………….12分
.……………….12分
 =
=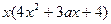 ,
,当
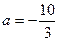 时
时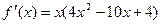 =
=
令
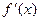 =0,解得
=0,解得 .
.?
当x变化时,f′(x),f(x)的变化情况如下表:
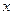 | 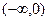 | 0 | 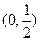 | 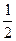 | (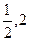 ) ) | 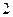 | 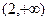 |
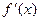 | _ | 0 | + | 0 | - | 0 | + |
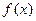 | 单调 递减 | 极小值 | 单调 递增 | 极大值 | 单调 递减 | 极小 值 | 单调 递增 |
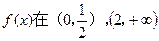 内是增函数,
内是增函数,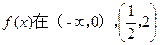 内是减函数……….4分
内是减函数……….4分
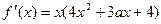 ,显然
,显然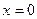 不是方程
不是方程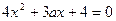 的根,为使
的根,为使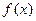
仅在
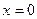 处有极值,必须有
处有极值,必须有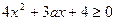 恒成立,即有
恒成立,即有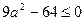 ,解得
,解得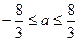 ,
,这时
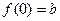 是唯一极值。因此,满足条件的a的取值范围是
是唯一极值。因此,满足条件的a的取值范围是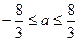 .………….8分
.………….8分(3)由条件
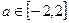 可知
可知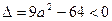 ,从而
,从而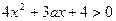 恒成立.
恒成立. 当
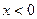 时,
时,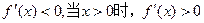 。
。因此函数
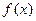 在
在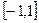 上的最大值是
上的最大值是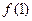 与
与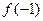 两者中的最大者。
两者中的最大者。为使对任意的
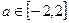 ,不等式
,不等式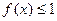 在
在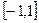 上恒成立,
上恒成立,当且仅当
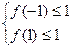 ,即
,即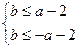 ,
,所以
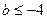 ,因此满足条件的
,因此满足条件的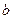 的取值范围是
的取值范围是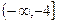 .……………….12分
.……………….12分略

练习册系列答案
相关题目
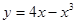 在点
在点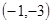 处的切线方程是 _ .
处的切线方程是 _ .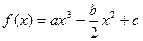 ,其图像过点(0,1).
,其图像过点(0,1).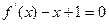 的两个根分别为是
的两个根分别为是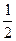 ,1时,求f(x)的解析式;
,1时,求f(x)的解析式;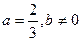 时,求函数f(x)的极大值与极小值.
时,求函数f(x)的极大值与极小值. 与时间错误!不能通过编辑域代码创建对象。的关系为
与时间错误!不能通过编辑域代码创建对象。的关系为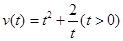 ,则
,则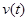 最小值为
最小值为 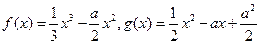 。
。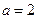 时,求曲线
时,求曲线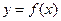 在点
在点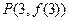 处的切线方程;
处的切线方程;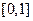 上的最小值为
上的最小值为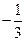 时,求实数
时,求实数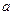 的值;
的值;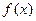 与
与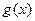 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数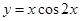 在点
在点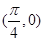 处的切线方程是( )
处的切线方程是( )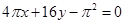
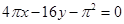
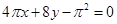
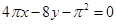
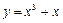 在点(1,2)处的切线与直线
在点(1,2)处的切线与直线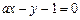 在
在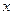 轴的截距相等,则
轴的截距相等,则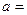 .
.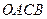 内的阴影区域的上边界是曲线
内的阴影区域的上边界是曲线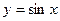 ,现向正方形区域内随机等可能地投点,则点落在阴影区域的概率是( *** )
,现向正方形区域内随机等可能地投点,则点落在阴影区域的概率是( *** )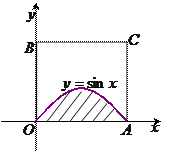
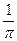
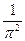
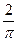
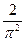
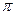 x)2的导数是( )
x)2的导数是( )