题目内容
【题目】已知函数![]() 在定义域内有两个不同的极值点.
在定义域内有两个不同的极值点.
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)记两个极值点为![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
(Ⅰ)由题意,方程![]() 在
在![]() 有两个不同根,即方程
有两个不同根,即方程![]() 有两个不同根;解法1:转化为函数
有两个不同根;解法1:转化为函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,解法2:转化为函数
上有两个不同交点,解法2:转化为函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点;解法3;求出
上有两个不同交点;解法3;求出![]() ,讨论
,讨论![]() 的取值范围,求出函数
的取值范围,求出函数![]() 的单调区间即可求解. (Ⅱ)由(Ⅰ)知:由(Ⅰ)知:
的单调区间即可求解. (Ⅱ)由(Ⅰ)知:由(Ⅰ)知:![]() 是
是![]() 的两个根,
的两个根, ![]() ,然后利用分析法要证
,然后利用分析法要证![]() ,只需证:
,只需证:![]() ,从而可得
,从而可得![]() ,进而可得
,进而可得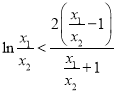 ,令
,令![]() ,换元转化为函数,利用函数的最值即可证出.
,换元转化为函数,利用函数的最值即可证出.
(Ⅰ)由题意,方程![]() 在
在![]() 有两个不同根,即方程
有两个不同根,即方程![]() 有两个不同根;
有两个不同根;
解法1:转化为函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,
上有两个不同交点,
令![]() ,
,
故![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]()
代入点![]() 有:
有:![]()
可得:![]()
解法2:转化为函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点.
上有两个不同交点.
![]() ,故
,故![]() 时,
时,![]()
![]() 时,
时,![]()
故![]() 在
在![]() 上单增,在
上单增,在![]() 上单减,
上单减,
![]()
又![]() ,故
,故![]() 时,
时,![]()
![]() 时,
时,![]()
可得:![]() …
…
解法3:![]()
①![]() 时,
时,![]() 故
故![]() 在
在![]() 上单增,
上单增,
故![]() 在
在![]() 最多只有一个实根,不合题意;
最多只有一个实根,不合题意;
②![]() 时,令
时,令![]() 令
令![]()
故![]() 在
在![]() 上单增,在
上单增,在![]() 上单减;
上单减;
故![]()
当![]() 时,
时, ![]()
故![]() 在
在![]() 上有两个不相等的实根,故
上有两个不相等的实根,故![]()
(Ⅱ)由(Ⅰ)知:![]() 是
是![]() 的两个根,
的两个根,
故![]()
要证:![]() ,只需证:
,只需证:![]() ,
,
即证:![]()
即证:![]() ,即证:
,即证:![]()
又![]() 故上式为:
故上式为: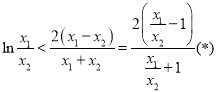
令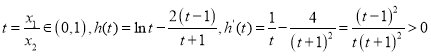
故![]() 在
在![]() 上单增,故
上单增,故![]() 故
故![]() 式成立,即证.
式成立,即证.

【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
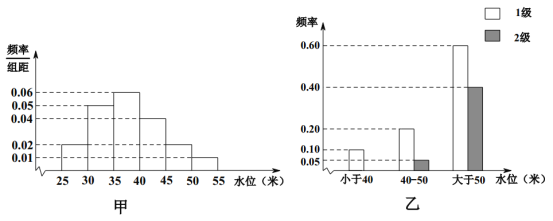
(1)试估计该河流在8月份水位的众数;
(2)我们知道若该河流8月份的水位小于40米的频率为f,该河流8月份的水位小于40米的情况下发生1级灾害的频率为g,则该河流8月份的水位小于40且发生1级灾害的频率为![]() ,其他情况类似.据此,试分别估计该河流在8月份发生12级灾害及不发生灾害的频率
,其他情况类似.据此,试分别估计该河流在8月份发生12级灾害及不发生灾害的频率![]() ,
,![]() ,
,![]() ;
;
(3)该河流域某企业,在8月份,若没受12级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
【题目】某公司准备加大对一项产品的科技改造,经过充分的市场调研与模拟,得到x,y之间的一组数,其中x(单位:百万元)是科技改造的总投入,y(单位:百万元)是改造后的额外收益
x | 2 | 3 | 5 | 7 | 8 |
y | 5 | 8 | 12 | 14 | 16 |
其中![]() ,
,![]() ,
,![]() 是对当地GDP的增长贡献值.
是对当地GDP的增长贡献值.
(1)若从五组数据中任取两组,求至少有一组满足![]() 的概率;
的概率;
(2)对于表中数据,甲、乙两个同学给出的拟合直线方程为:![]() ,
,![]() ,试用最小二乘法判断哪条直线的拟合程度更好.(附:
,试用最小二乘法判断哪条直线的拟合程度更好.(附:![]() ;Q越小拟合度越好.)
;Q越小拟合度越好.)